Dựa vào thông tin dưới đây để trả lời các câu từ 72 đến 73
Một xưởng chuyên sản xuất hai loại sản phẩm, sản phẩm A và sản phẩm B. Để sản xuất cả hai loại sản phẩm, xưởng có thể sử dụng tối đa 150 kg nguyên liệu và tối đa 120 giờ lao động. Biết rằng để sản xuất 1 đơn vị sản phẩm \(A\) cần 4 kg nguyên liệu, 2 giờ lao động và lợi nhuận là \(70\,000\) đồng; để sản xuất 1 đơn vị sản phẩm \(B\) cần 3 kg nguyên liệu, 4 giờ lao động và lợi nhuận là \(50\,000\) đồng.
Để đạt được lợi nhuận cao nhất, xưởng đã sản xuất \(a\) (đơn vị) sản phẩm A và \(b\) (đơn vị) sản phẩm B. Giá trị của \(a\) là:
Dựa vào thông tin dưới đây để trả lời các câu từ 72 đến 73
Một xưởng chuyên sản xuất hai loại sản phẩm, sản phẩm A và sản phẩm B. Để sản xuất cả hai loại sản phẩm, xưởng có thể sử dụng tối đa 150 kg nguyên liệu và tối đa 120 giờ lao động. Biết rằng để sản xuất 1 đơn vị sản phẩm \(A\) cần 4 kg nguyên liệu, 2 giờ lao động và lợi nhuận là \(70\,000\) đồng; để sản xuất 1 đơn vị sản phẩm \(B\) cần 3 kg nguyên liệu, 4 giờ lao động và lợi nhuận là \(50\,000\) đồng.
Để đạt được lợi nhuận cao nhất, xưởng đã sản xuất \(a\) (đơn vị) sản phẩm A và \(b\) (đơn vị) sản phẩm B. Giá trị của \(a\) là:Quảng cáo
Trả lời:
Điều kiện: \(a \ge 0\,;\,\,b \ge 0\,;\,\,a\,,\,b \in \mathbb{Z}\).
Ràng buộc nguyên liệu: \(4a + 3b \le 150\).
Ràng buộc số giờ lao động: \(2a + 4b \le 120\).
Lợi nhuận: \(T\left( {a;\,b} \right) = 70\,000a + 50\,000b\) (đồng).
Bài toán đã cho trở thành tìm \(\left( {a\,;\,b} \right)\) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}4a + 3b \le 150\\2a + 4b \le 120\\a \ge 0\\b \ge 0\end{array} \right.\) để \(T\left( {a\,;\,b} \right)\) đạt giá trị lớn nhất.
Miền nghiệm của hệ bất phương trình trên là miền tứ giác \(OABC\) với \(O\left( {0\,;\,0} \right)\), \(A\left( {37,5\,;\,0} \right)\), \(B\left( {24\,;\,18} \right)\) và \(C\left( {0\,;\,30} \right)\).
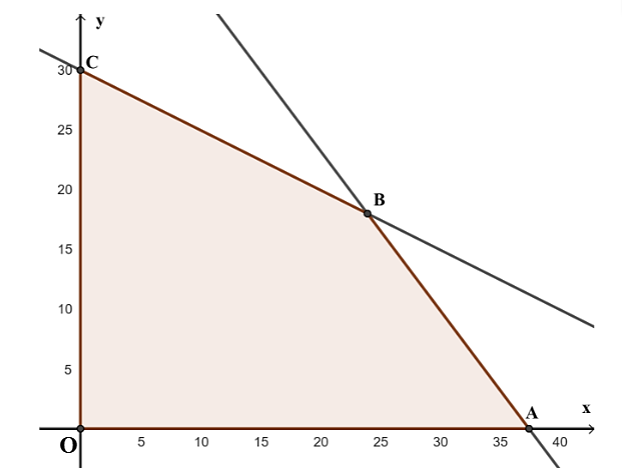
Ta có \(T\left( {0\,;\,0} \right) = 0\); \(T\left( {24\,;\,18} \right) = 70\,000 \cdot 24 + 50\,000 \cdot 18 = 2\,580\,000\);
\(T\left( {0\,;\,30} \right) = 70\,000 \cdot 0 + 50\,000 \cdot 30 = 1\,500\,000\).
Vì \(37,5 \notin \mathbb{Z}\) nên ta chọn điểm \(\left( {37\,;\,0} \right)\), có \(T\left( {37\,;\,0} \right) = 70\,000 \cdot 37 + 50\,000 \cdot 0 = 2\,590\,000\).
Lợi nhuận lớn nhất là tại điểm \(\left( {37\,;\,0} \right)\). Vậy \(a = 37\). Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
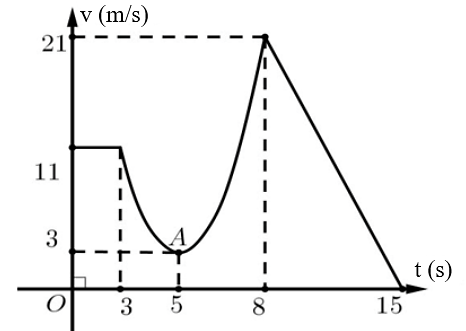
Gọi hàm vận tốc thời gian \(t\) giây \[\left( {3 \le t \le 8} \right)\]có dạng là \(\left( P \right):v\left( t \right) = a{t^2} + bt + c\).
\(\left( P \right)\) đi qua các điểm: \[\left( {3\,;11} \right)\]; \[\left( {5\,;3} \right)\]; \[\left( {8\,;21} \right)\] nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}9a + 3b + c = 11\\25a + 5b + c = 3\\64a + 8b + c = 21\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 20\\c = 53\end{array} \right.\) \( \Rightarrow \left( P \right):v\left( t \right) = 2{t^2} - 20t + 53\).
Quãng đường chất điểm đi được trong thời gian \(t\) giây \[\left( {3 \le t \le 8} \right)\] là:
\(S' = \int\limits_3^8 {\left( {2{t^2} - 20t + 53} \right)\,{\rm{d}}t = \frac{{115}}{3}} \,\,(m)\).
Vận tốc trung bình của chất điểm trong thời gian \[t\] giây \[\left( {3 \le t \le 8} \right)\] là:
\[\frac{{115}}{3}:\left( {8 - 3} \right) = \frac{{23}}{3}\] (\[{\rm{m/s}}\]). Chọn B.
Câu 2
Lời giải
Gọi hàm vận tốc thời gian \(7\) giây cuối \[\left( {8 \le t \le 15} \right)\] có dạng là \[\left( d \right):{\rm{ }}v\left( t \right) = {\rm{ }}at + b\].
Đường thẳng \[\left( d \right)\] đi qua hai điểm \[\left( {8\,;21} \right)\] và \[\left( {15\,;0} \right)\] nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}8a + b = 21\\15a + b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = 45\end{array} \right.\)\[ \Rightarrow \left( d \right):v\left( t \right) = - 3t + 45\].
Quãng đường chất điểm đi được trong thời gian \[7\] giây cuối \[\left( {8 \le t \le 15} \right)\] là:
\(S = \int\limits_8^{15} {v\left( t \right)dt} = \int\limits_8^{15} {\left( { - 3t + 45} \right)\,dt = 73,5\,\,(m)} \). Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.