Dựa vào thông tin dưới đây để trả lời các câu từ 74 đến 75
Cho hình vuông \(ABCD\) cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho \(AM = \frac{1}{4}AC\).
Diện tích tam giác BMN bằng
Dựa vào thông tin dưới đây để trả lời các câu từ 74 đến 75
Cho hình vuông \(ABCD\) cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho \(AM = \frac{1}{4}AC\).
Diện tích tam giác BMN bằngQuảng cáo
Trả lời:
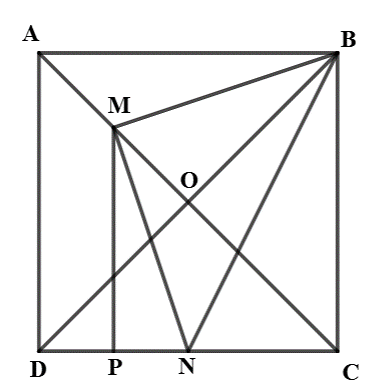
Ta có \(NC = \frac{{DC}}{2} = \frac{a}{2}\);
\(BN = \sqrt {B{C^2} + N{C^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\).
Gọi O là tâm của hình vuông \(ABCD\).
Khi đó, \(BO = \frac{{BD}}{2} = \frac{{a\sqrt 2 }}{2};\,MO = \frac{{AO}}{2} = \frac{{a\sqrt 2 }}{4}\).
Do đó, \(BM = \sqrt {M{O^2} + B{O^2}} = \frac{{a\sqrt {10} }}{4}\).Từ M, kẻ MP // AD \(\left( {P \in CD} \right)\). Áp dụng định lí Thalès trong tam giác CAD, ta được:
\(\frac{{MP}}{{AD}} = \frac{{CP}}{{CD}} = \frac{{CM}}{{CA}} = \frac{3}{4} \Rightarrow MP = \frac{3}{4}AD = \frac{{3a}}{4}\); \(CP = \frac{3}{4}CD = \frac{{3a}}{4}\).
Lại có \(CN + NP = CP\) nên \(NP = CP - CN = \frac{{3a}}{4} - \frac{a}{2} = \frac{a}{4}\).
Khi đó, \(MN = \sqrt {M{P^2} + N{P^2}} = \frac{{a\sqrt {10} }}{4}\).
Nhận thấy tam giác BMN vuông cân tại M nên \({S_{BMN}} = \frac{1}{2}BM \cdot MN = \frac{{5{a^2}}}{{16}}\). Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
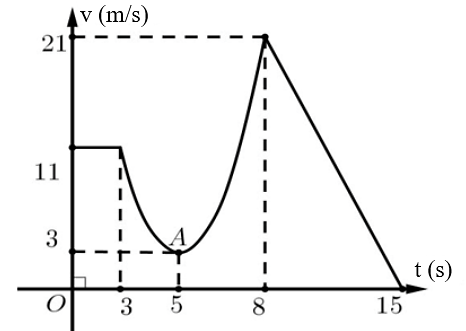
Gọi hàm vận tốc thời gian \(t\) giây \[\left( {3 \le t \le 8} \right)\]có dạng là \(\left( P \right):v\left( t \right) = a{t^2} + bt + c\).
\(\left( P \right)\) đi qua các điểm: \[\left( {3\,;11} \right)\]; \[\left( {5\,;3} \right)\]; \[\left( {8\,;21} \right)\] nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}9a + 3b + c = 11\\25a + 5b + c = 3\\64a + 8b + c = 21\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 20\\c = 53\end{array} \right.\) \( \Rightarrow \left( P \right):v\left( t \right) = 2{t^2} - 20t + 53\).
Quãng đường chất điểm đi được trong thời gian \(t\) giây \[\left( {3 \le t \le 8} \right)\] là:
\(S' = \int\limits_3^8 {\left( {2{t^2} - 20t + 53} \right)\,{\rm{d}}t = \frac{{115}}{3}} \,\,(m)\).
Vận tốc trung bình của chất điểm trong thời gian \[t\] giây \[\left( {3 \le t \le 8} \right)\] là:
\[\frac{{115}}{3}:\left( {8 - 3} \right) = \frac{{23}}{3}\] (\[{\rm{m/s}}\]). Chọn B.
Câu 2
Lời giải
Gọi hàm vận tốc thời gian \(7\) giây cuối \[\left( {8 \le t \le 15} \right)\] có dạng là \[\left( d \right):{\rm{ }}v\left( t \right) = {\rm{ }}at + b\].
Đường thẳng \[\left( d \right)\] đi qua hai điểm \[\left( {8\,;21} \right)\] và \[\left( {15\,;0} \right)\] nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}8a + b = 21\\15a + b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = 45\end{array} \right.\)\[ \Rightarrow \left( d \right):v\left( t \right) = - 3t + 45\].
Quãng đường chất điểm đi được trong thời gian \[7\] giây cuối \[\left( {8 \le t \le 15} \right)\] là:
\(S = \int\limits_8^{15} {v\left( t \right)dt} = \int\limits_8^{15} {\left( { - 3t + 45} \right)\,dt = 73,5\,\,(m)} \). Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.