PHẦN 1: SỬ DỤNG NGÔN NGỮ

1.1. TIẾNG VIỆT (30 CÂU)

Câu nào trong các câu thơ sau sử dụng hình ảnh ước lệ?    

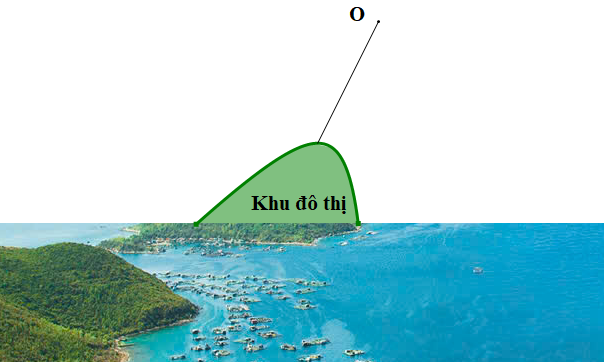
Độ dài ngắn nhất của tuyến cáp treo nối với đường bao của khu đô thị chính là khoảng cách từ \(O\) tới điểm cực đại của đồ thị hàm số \(y = \frac{{{x^2} + 1}}{x}\).

Xét hàm số \(y = \frac{{{x^2} + 1}}{x}\) với \(x \ne 0\).

Ta có \(y' = \frac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow x = - 1\) hoặc \[x = 1\].

Bảng biến thiên:

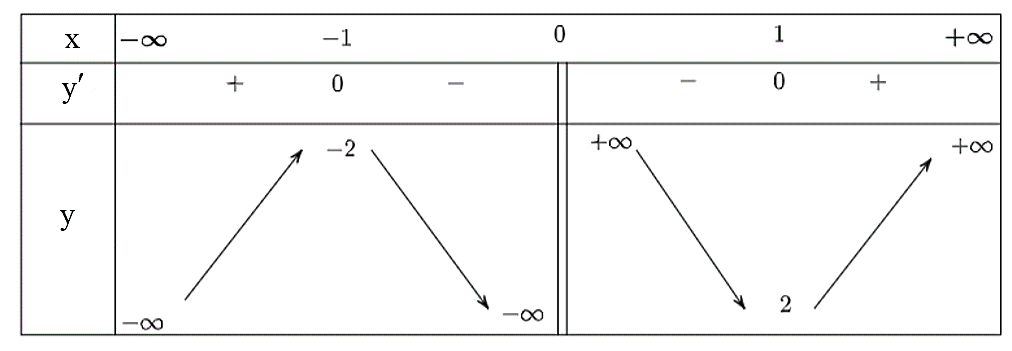
Dựa vào bảng biến thiên, đồ thị hàm số có điểm cực đại là \(A\left( { - 1; - 2} \right)\).

Khi đó \(OA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \approx 2,2\).

Vậy độ dài của tuyến cáp treo xấp xỉ \(2,2\)km. Chọn A.

Đặt \(0 < \alpha < \pi \) thỏa \(\cos \alpha = \frac{{2024}}{{2025}}.\) Khi đó,

\(\cos \left( {2018x} \right) = \frac{{2024}}{{2025}} \Leftrightarrow \cos \left( {2018x} \right) = \cos \alpha \)

\( \Leftrightarrow \left[ \begin{array}{l}2018x = \alpha + k2\pi \\2018x = - \alpha + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\alpha }{{2018}} + k\frac{\pi }{{1009}}\\x = - \frac{\alpha }{{2018}} + k\frac{\pi }{{1009}}\end{array} \right.\left( {k \in \mathbb{Z}} \right).\)

Với \(x \in \left( {0\,;\,2\pi } \right)\), ta có

+ Trường hợp 1: \(0 < \frac{\alpha }{{2018}} + k\frac{\pi }{{1009}} < 2\pi \Leftrightarrow - \frac{\alpha }{{2\pi }} < k < 2018 - \frac{\alpha }{{2\pi }} \Leftrightarrow 0 \le k \le 2017\)

(Vì \(0 < \alpha < \pi \Leftrightarrow \frac{0}{{2\pi }} < \frac{\alpha }{{2\pi }} < \frac{\pi }{{2\pi }} \Leftrightarrow 0 < \frac{\alpha }{{2\pi }} < \frac{1}{2}\)).

Nên có \(2018\) giá trị \(k.\)

+ Trường hợp 2: \(0 < - \frac{\alpha }{{2018}} + k\frac{\pi }{{1009}} < 2\pi \Leftrightarrow \frac{\alpha }{{2\pi }} < k < \frac{\alpha }{{2\pi }} + 2018 \Leftrightarrow 1 \le k \le 2018\).

Nên có \(2018\) giá trị \(k.\)

Dễ dàng thấy các nghiệm ở trường hợp 1 không trùng với nghiệm nào của trường hợp 2.

Vậy phương trình có \(4036\) nghiệm thực thuộc khoảng \(\left( {0\,;\,2\pi } \right)\). Chọn D.