Một buổi hầu rồi một buổi ngơi,

                                         Đâu còn nhớ chữ “viễn phương lai”.

                                         Mới sang chừng ấy ngơi chừng ấy,

                                         Sang nữa thì ngơi biết mấy đời.

(Cao Bá Quát, Quan ngơi)

Xác định thể thơ của bài thơ?    

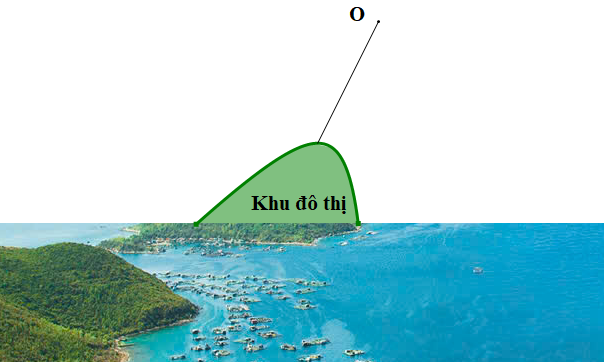
Độ dài ngắn nhất của tuyến cáp treo nối với đường bao của khu đô thị chính là khoảng cách từ \(O\) tới điểm cực đại của đồ thị hàm số \(y = \frac{{{x^2} + 1}}{x}\).

Xét hàm số \(y = \frac{{{x^2} + 1}}{x}\) với \(x \ne 0\).

Ta có \(y' = \frac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow x = - 1\) hoặc \[x = 1\].

Bảng biến thiên:

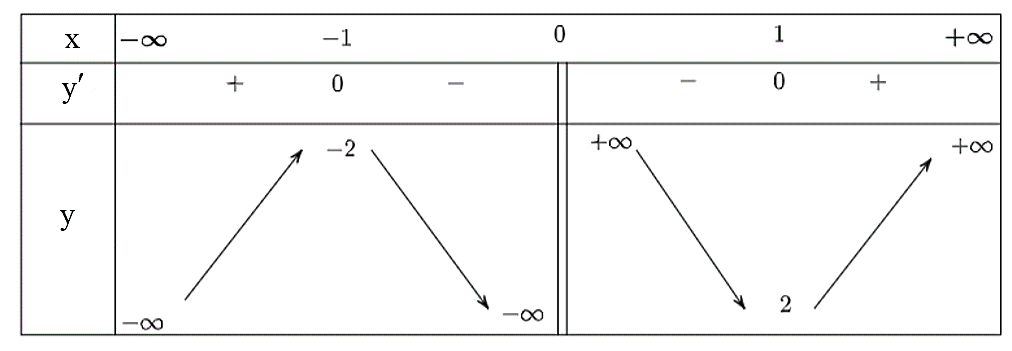
Dựa vào bảng biến thiên, đồ thị hàm số có điểm cực đại là \(A\left( { - 1; - 2} \right)\).

Khi đó \(OA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \approx 2,2\).

Vậy độ dài của tuyến cáp treo xấp xỉ \(2,2\)km. Chọn A.

Gọi \(p = ax + b\,\,\left( * \right)\), với \(x\) là số sản phẩm \(A\) bán ra.

Vì sản phẩm \(A\) bán với giá \(100\) nghìn đồng thì có \(290\) người mua nên ta có \(p = 100,x = 290\) thay vào \(\left( * \right)\) ta có \(290a + b = 100\) (1).

Vì cứ giảm \(10\) nghìn đồng thì lại có thêm \(50\) người mua nên ta có \(p = 90,x = 340\) thay vào \(\left( * \right)\) ta có \(340a + b = 90\) (2).

Từ (1), (2) ta có hệ phương trình \(\left\{ \begin{array}{l}290a + b = 100\\340a + b = 90\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{5}\\b = 158\end{array} \right.\).

Ta có \(p = - \frac{1}{5}x + 158 \Leftrightarrow x = 790 - 5p\).

Vậy số sản phẩm \(A\) bán ra là \(790 - 5p\). Chọn A.