Dựa vào thông tin dưới đây để trả lời các câu sau từ câu 106 - 108:
- Chất khí được cấu tạo từ các phân tử có kích thước rất nhỏ so với khoảng cách giữa chúng.
- Các phân tử khí chuyển động hỗn loạn, không ngừng; các phân tử khí chuyển động càng nhanh thì nhiệt độ chất khí càng cao.
- Khi chuyển động hỗn loạn, các phân tử khí va chạm vào thành bình gây áp suất lên thành bình.
Một phòng trống có kích thước 5,0 m × 10,0 m × 3,0 m. Lúc đầu, không khí trong phòng ở điều kiện tiêu chuẩn (nhiệt độ 0,0 °C và áp suất 1,0.105 Pa) và có khối lượng mol là 29 g/mol.
Khi quan sát các hạt khói chuyển động lơ lửng trong không khí thì
Dựa vào thông tin dưới đây để trả lời các câu sau từ câu 106 - 108:
- Chất khí được cấu tạo từ các phân tử có kích thước rất nhỏ so với khoảng cách giữa chúng.
- Các phân tử khí chuyển động hỗn loạn, không ngừng; các phân tử khí chuyển động càng nhanh thì nhiệt độ chất khí càng cao.
- Khi chuyển động hỗn loạn, các phân tử khí va chạm vào thành bình gây áp suất lên thành bình.
Một phòng trống có kích thước 5,0 m × 10,0 m × 3,0 m. Lúc đầu, không khí trong phòng ở điều kiện tiêu chuẩn (nhiệt độ 0,0 °C và áp suất 1,0.105 Pa) và có khối lượng mol là 29 g/mol.
Khi quan sát các hạt khói chuyển động lơ lửng trong không khí thì
Quảng cáo
Trả lời:
Chọn B
Khi quan sát các hạt khói chuyển động lơ lửng trong không khí thì chuyển động của các hạt khói được gọi là chuyển động Brown.
Câu hỏi cùng đoạn
Câu 2:
Xác định số mol và khối lượng không khí có trong phòng. Biết hằng số khí lí tưởng là R = 8,31 J.mol-1K-1.
Chọn C
pV = nRT → số mol không khí trong phòng là \[n = \frac{{pV}}{{RT}} = \frac{{{{10}^5}.5.10.3}}{{8,31.273}} = 6,{6.10^3}mol\].
Khối lượng không khí trong phòng là m = n.μ = 6,6.103.29 = 1,9.105 g = 1,9.102 kg.
Câu 3:
Khi mở cửa phòng thì nhiệt độ phòng tăng lên 20 °C và áp suất khí trong phòng bằng áp suất bên ngoài phòng là 0,9.105 Pa. Tính khối lượng không khí trong phòng đã thoát ra ngoài.
Chọn A
\[\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Rightarrow \frac{{{{10}^5}.5.10.3}}{{273}} = \frac{{0,{{9.10}^5}.{V_2}}}{{20 + 273}} \Rightarrow {V_2} \approx 179\,{m^3}\]
Như vậy, đã có DV = 179 – 5.10.3 = 29 m3 khí ở nhiệt độ 20 °C và áp suất 0,9.105 Pa thoát ra khỏi phòng.
Khối lượng không khí trong phòng đã thoát ra ngoài bằng:
\(\Delta m = \frac{{29}}{{179}}m = \frac{{29}}{{179}}\left( {1,9 \cdot {{10}^2}\;{\rm{g}}} \right) \approx 30\;{\rm{g}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
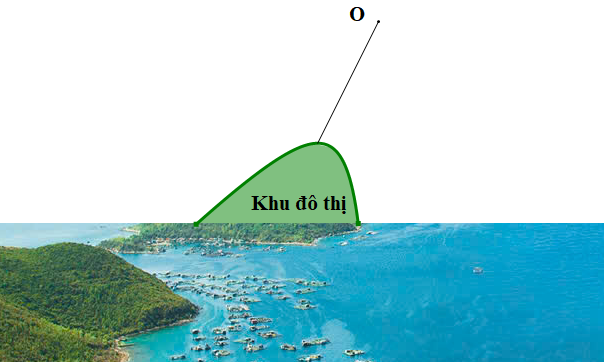
Độ dài ngắn nhất của tuyến cáp treo nối với đường bao của khu đô thị chính là khoảng cách từ \(O\) tới điểm cực đại của đồ thị hàm số \(y = \frac{{{x^2} + 1}}{x}\).
Xét hàm số \(y = \frac{{{x^2} + 1}}{x}\) với \(x \ne 0\).
Ta có \(y' = \frac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow x = - 1\) hoặc \[x = 1\].
Bảng biến thiên:
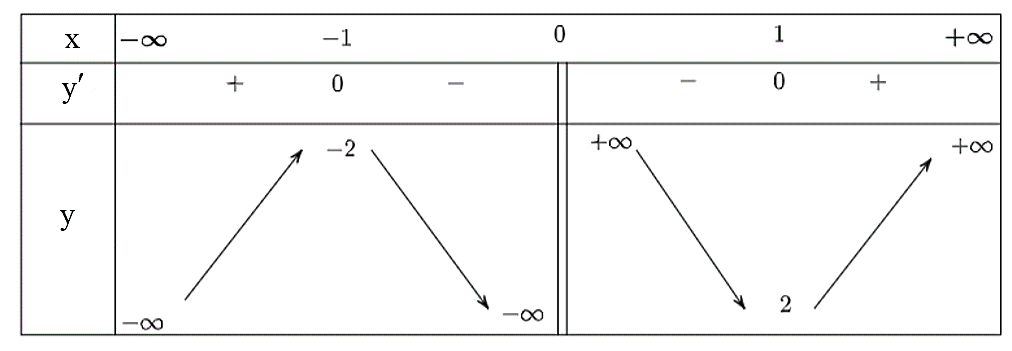
Dựa vào bảng biến thiên, đồ thị hàm số có điểm cực đại là \(A\left( { - 1; - 2} \right)\).
Khi đó \(OA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \approx 2,2\).
Vậy độ dài của tuyến cáp treo xấp xỉ \(2,2\)km. Chọn A.
Câu 2
Lời giải
Gọi \(p = ax + b\,\,\left( * \right)\), với \(x\) là số sản phẩm \(A\) bán ra.
Vì sản phẩm \(A\) bán với giá \(100\) nghìn đồng thì có \(290\) người mua nên ta có \(p = 100,x = 290\) thay vào \(\left( * \right)\) ta có \(290a + b = 100\) (1).
Vì cứ giảm \(10\) nghìn đồng thì lại có thêm \(50\) người mua nên ta có \(p = 90,x = 340\) thay vào \(\left( * \right)\) ta có \(340a + b = 90\) (2).
Từ (1), (2) ta có hệ phương trình \(\left\{ \begin{array}{l}290a + b = 100\\340a + b = 90\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{5}\\b = 158\end{array} \right.\).
Ta có \(p = - \frac{1}{5}x + 158 \Leftrightarrow x = 790 - 5p\).
Vậy số sản phẩm \(A\) bán ra là \(790 - 5p\). Chọn A.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.