Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy S = 25π cm2 và chiều cao h = 10 cm. Nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?
A. 1200π (cm2).
B. 600π (cm2).
C. 1000π (cm2).
D. 1210π (cm2).
Quảng cáo
Trả lời:
Đáp án đúng là: A
Bán kính của trục lăn này là: \[\sqrt {25\pi :\pi } \] = 5 (cm).
Diện tích xung quanh của trục lăn là: Sxq = 2πrh = 2π.5.10 = 100π (cm2).
Diện tích trên sân phẳng khi trục lăn 12 vòng là: 100π.12 = 1200π (cm2).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[\frac{{3456}}{5}\pi \] cm2.
B. \[\frac{{3456}}{{25}}\pi \] cm2.
C. \[\frac{{1728}}{{25}}\pi \] cm2.
D. \[\frac{{7128}}{{25}}\pi \] cm2.
Lời giải
Đáp án đúng là: B
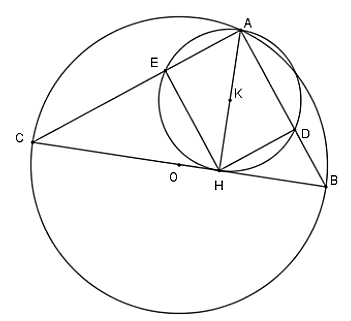
Xét ∆HAC và ∆HBA, có:
\[\widehat {AHC} = \widehat {AHB} = 90^\circ \] (gt)
\[\widehat {ACH} = \widehat {HAB}\] (cùng phụ với góc CAH)
Suy ra ∆HAC ᔕ ∆HBA (g.g)
Do đó, HC.HB = AH2 hay HB.HC = 122 = 144 (1)
Lại có HB + HC = BC nên HB + HC = 25 (2)
Từ (1) và (2) tính được HB = 9 cm và HC = 16 cm (Do AB < AC nên HB < HC).
Xét tam giác AHB vuông tại H có HD ⊥ AB nên ta chứng minh được
∆HAD ᔕ ∆BHD (g.g)
Suy ra \[\frac{{HD}}{{BD}} = \frac{{HA}}{{BH}} = \frac{{AD}}{{HD}}\] (tỉ lệ các cạnh tương ứng).
Áp dụng đinhk lý Pythagore vào tam giác HAB vuông tại H, ta có:
AH2 + HB2 = AB2 nên AB2 = 122 + 92 suy ra AB2 = 225 và AB = 15 cm.
Có tam giác AHB vuông tại H nên SAHB = \[\frac{1}{2}\]AH.HB = \[\frac{1}{2}\]HD.AB,
Suy ra AH.HB = HD.AB nên HD = \[\frac{{AH.HB}}{{AB}} = \frac{{12.9}}{{15}} = \frac{{36}}{5}\] cm.
Do đó, HD = \[\frac{{36}}{5}\] cm.
Tương tự, tính được HE = \[\frac{{48}}{5}\] cm nên AD = \[\frac{{48}}{5}\] cm.
Khi quay hình chữ nhật ADHE quanh AD ta được hình trụ có chiều cao AD, bán kính đáy HD nên Sxq = 2π.HD.AD = \[\frac{{3456}}{{25}}\pi \] (cm2).
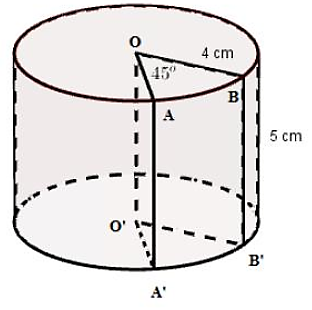
Câu 2
A. 70π (cm3).
B. 30π (cm3).
C. 60π (cm3).
D. 10π (cm3).
Lời giải
Đáp án đúng là: A
Thể tích hình trụ ban đầu là: V = πr2h = 80π (cm3).
Diện tích phần đáy hình quạt của phần hình bị cắt OABB'A'O' là
S = \[\frac{{\pi {r^2}n}}{{360}} = \frac{{\pi .16.45}}{{360}} = 2\pi \] (cm2).
Thể tích phần hình bị cắt OABB'A'O' là V = 2π.5 = 10π (cm3).
Do đó, thể tích của phần còn lại là: 80π – 10π = 70π (cm3).
Câu 3
A. 110π (cm2).
B. 129π (cm2).
C. 96π (cm2).
D. 69π (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 7 cm.
B. 5 cm.
C. 3 cm.
D. 9 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 2 cm.
B. 4 cm.
C. 1 cm.
D. 8 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Cho hình trụ có bán kính r = 12 (cm) và diện tích toàn phần 672π (cm2). Tính chiều cao của hình trụ.
A. 16 cm.
B. 18 cm.
C. 8 cm.
D. 10 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.