Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O; R) đường kính BC. Vẽ đường cao AH của tam giác ABC. Đường tròn tâm K đường kính AH cắt AB, AC lần lượt tại D và E. Biết BC = 25 cm và AH = 12 cm. Hãy tính diện tích xung quanh của hình tạo bởi khi cho tứ giác ADHE quay quanh AD.
A. \[\frac{{3456}}{5}\pi \] cm2.
B. \[\frac{{3456}}{{25}}\pi \] cm2.
C. \[\frac{{1728}}{{25}}\pi \] cm2.
D. \[\frac{{7128}}{{25}}\pi \] cm2.
Quảng cáo
Trả lời:
Đáp án đúng là: B
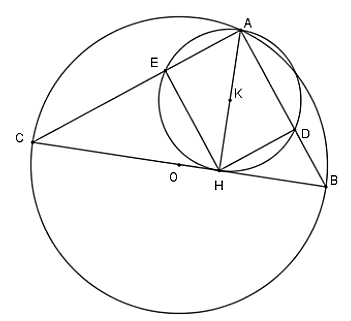
Xét ∆HAC và ∆HBA, có:
\[\widehat {AHC} = \widehat {AHB} = 90^\circ \] (gt)
\[\widehat {ACH} = \widehat {HAB}\] (cùng phụ với góc CAH)
Suy ra ∆HAC ᔕ ∆HBA (g.g)
Do đó, HC.HB = AH2 hay HB.HC = 122 = 144 (1)
Lại có HB + HC = BC nên HB + HC = 25 (2)
Từ (1) và (2) tính được HB = 9 cm và HC = 16 cm (Do AB < AC nên HB < HC).
Xét tam giác AHB vuông tại H có HD ⊥ AB nên ta chứng minh được
∆HAD ᔕ ∆BHD (g.g)
Suy ra \[\frac{{HD}}{{BD}} = \frac{{HA}}{{BH}} = \frac{{AD}}{{HD}}\] (tỉ lệ các cạnh tương ứng).
Áp dụng đinhk lý Pythagore vào tam giác HAB vuông tại H, ta có:
AH2 + HB2 = AB2 nên AB2 = 122 + 92 suy ra AB2 = 225 và AB = 15 cm.
Có tam giác AHB vuông tại H nên SAHB = \[\frac{1}{2}\]AH.HB = \[\frac{1}{2}\]HD.AB,
Suy ra AH.HB = HD.AB nên HD = \[\frac{{AH.HB}}{{AB}} = \frac{{12.9}}{{15}} = \frac{{36}}{5}\] cm.
Do đó, HD = \[\frac{{36}}{5}\] cm.
Tương tự, tính được HE = \[\frac{{48}}{5}\] cm nên AD = \[\frac{{48}}{5}\] cm.
Khi quay hình chữ nhật ADHE quanh AD ta được hình trụ có chiều cao AD, bán kính đáy HD nên Sxq = 2π.HD.AD = \[\frac{{3456}}{{25}}\pi \] (cm2).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 1200π (cm2).
B. 600π (cm2).
C. 1000π (cm2).
D. 1210π (cm2).
Lời giải
Đáp án đúng là: A
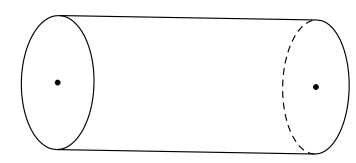
Bán kính của trục lăn này là: \[\sqrt {25\pi :\pi } \] = 5 (cm).
Diện tích xung quanh của trục lăn là: Sxq = 2πrh = 2π.5.10 = 100π (cm2).
Diện tích trên sân phẳng khi trục lăn 12 vòng là: 100π.12 = 1200π (cm2).
Câu 2
A. 70π (cm3).
B. 30π (cm3).
C. 60π (cm3).
D. 10π (cm3).
Lời giải
Đáp án đúng là: A
Thể tích hình trụ ban đầu là: V = πr2h = 80π (cm3).
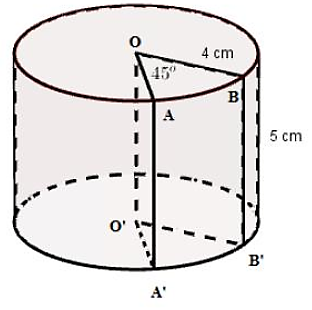
Diện tích phần đáy hình quạt của phần hình bị cắt OABB'A'O' là
S = \[\frac{{\pi {r^2}n}}{{360}} = \frac{{\pi .16.45}}{{360}} = 2\pi \] (cm2).
Thể tích phần hình bị cắt OABB'A'O' là V = 2π.5 = 10π (cm3).
Do đó, thể tích của phần còn lại là: 80π – 10π = 70π (cm3).
Câu 3
A. 110π (cm2).
B. 129π (cm2).
C. 96π (cm2).
D. 69π (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 7 cm.
B. 5 cm.
C. 3 cm.
D. 9 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 2 cm.
B. 4 cm.
C. 1 cm.
D. 8 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Cho hình trụ có bán kính r = 12 (cm) và diện tích toàn phần 672π (cm2). Tính chiều cao của hình trụ.
A. 16 cm.
B. 18 cm.
C. 8 cm.
D. 10 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.