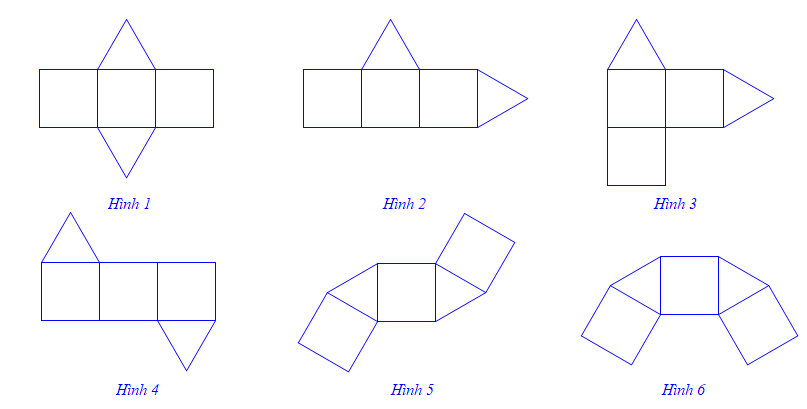
Trong các hình triển khai dưới đây, có bao nhiêu hình gấp lại được thành một hình lăng trụ đứng?

 

Hướng dẫn giải

a) Ta có: \(\frac{7}{5} + \frac{5}{7}.\left( { - \frac{7}{{25}}} \right) = \frac{7}{5} + \left( { - \frac{1}{5}} \right) = \frac{6}{5}.\)

b) Ta có: \(\left( { - \frac{3}{4} + \frac{2}{7}} \right):\frac{2}{3} + \left( { - \frac{1}{4} + \frac{5}{7}} \right):\frac{2}{3} = \left( { - \frac{3}{4} + \frac{2}{7}} \right).\frac{3}{2} + \left( { - \frac{1}{4} + \frac{5}{7}} \right).\frac{3}{2}\)

                                                              \( = \left( { - \frac{3}{4} + \frac{2}{7} + \frac{5}{7} - \frac{1}{4}} \right).\frac{3}{2}\)

                                                              \( = \left[ {\left( { - \frac{3}{4} - \frac{1}{4}} \right) + \left( {\frac{2}{7} + \frac{5}{7}} \right)} \right].\frac{3}{2}\)

                                                              \( = \left[ { - 1 + 1} \right].\frac{3}{2} = 0.\frac{3}{2} = 0\).

c) \(4.{\left( { - \frac{1}{2}} \right)^3} + \left| { - \frac{3}{2} + \sqrt {\frac{9}{4}} } \right|:\sqrt {0,25} = 4.\frac{{\left( { - 1} \right)}}{8} + \left| { - \frac{3}{2} + \frac{3}{2}} \right|:0,5 = \frac{{ - 1}}{2} + 0:0,5 = \frac{{ - 1}}{2} + 0 = \frac{{ - 1}}{2}.\)

Hướng dẫn giải

Đáp án đúng là: a) Đ            b) S            c) S             d) S

Số học sinh khá lớp 7A là: \(\frac{9}{{16}}.48 = 27\) (học sinh). Do đó, ý a) đúng.

Số học sinh giỏi và xuất sắc của lớp 7A là: \(48 - 27 = 21\) (học sinh). Do đó, ý b) đúng.

Ta có số học sinh giỏi bằng \(\frac{{11}}{{10}}\) số học sinh xuất sắc nên ta có số học sinh giỏi là:

\(21:\left( {11 + 10} \right).11 = 11\) (học sinh)

Số học sinh xuất sắc là: \(21 - 11 = 10\) (học sinh)

Số học sinh giỏi so với tổng số học sinh giỏi và xuất sắc là \(\frac{{11}}{{21}}\) (số học sinh). Do đóm ý c) sai.

Ta tính được số học sinh xuất sắc là 10 học sinh nên ý d) là sai.