Cho hình vuông \(ABCD\) có cạnh bằng 4 cm. Khi đó
a) \(AB = BC = CD = DA = 4{\rm{\;cm}}.\)
b) \(AC\) và \(BD\) song song với nhau.
c) Mỗi góc ở các đỉnh của hình vuông bằng nhau và bằng \(60^\circ .\)
d) Vẽ cạnh \(AB = 4{\rm{\;cm}}{\rm{.}}\) Dùng thước eke vẽ các đường vuông góc với \(AB\) tại \(A,\,\,B,\) sau đó lần lượt lấy các điểm \(D,\,\,C\) trên các đường đó sao cho \(AD = BC = 4{\rm{\;cm}}.\) Nối \(C\) với \(D\) ta được hình vuông \(ABCD\) có cạnh 4 cm như đã cho.
Cho hình vuông \(ABCD\) có cạnh bằng 4 cm. Khi đó
a) \(AB = BC = CD = DA = 4{\rm{\;cm}}.\)
b) \(AC\) và \(BD\) song song với nhau.
c) Mỗi góc ở các đỉnh của hình vuông bằng nhau và bằng \(60^\circ .\)
d) Vẽ cạnh \(AB = 4{\rm{\;cm}}{\rm{.}}\) Dùng thước eke vẽ các đường vuông góc với \(AB\) tại \(A,\,\,B,\) sau đó lần lượt lấy các điểm \(D,\,\,C\) trên các đường đó sao cho \(AD = BC = 4{\rm{\;cm}}.\) Nối \(C\) với \(D\) ta được hình vuông \(ABCD\) có cạnh 4 cm như đã cho.
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: a) Đúng. b) Sai. c) Sai. d) Đúng.
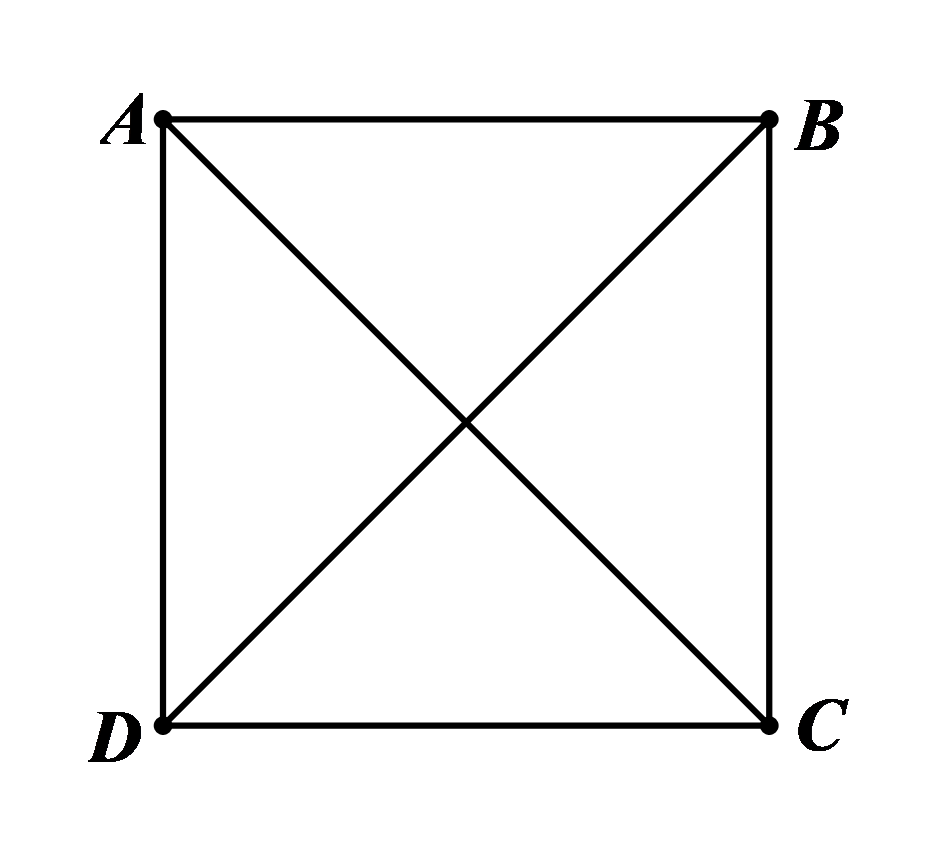
⦁ Hình vuông \(ABCD\) có cạnh bằng 4 cm nên \(AB = BC = CD = DA = 4{\rm{\;cm}}.\) Do đó ý a) là khẳng định đúng.
⦁ Hình vuông \(ABCD\) có \(AC\) và \(BD\) là hai đường chéo nên không song song với nhau mà cắt nhau. Do đó ý b) là khẳng định sai.
⦁ Hình vuông \(ABCD\) có mỗi góc ở các đỉnh của hình vuông bằng nhau và bằng \(90^\circ .\) Do đó ý c) là khẳng định đúng.
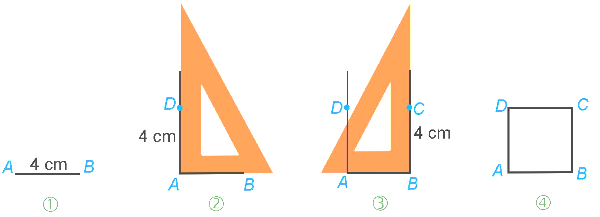
⦁ Vẽ cạnh \(AB = 4{\rm{\;cm}}\) (Hình j). Dùng thước eke vẽ các đường vuông góc với \(AB\) tại \(A,\,\,B,\) sau đó lần lượt lấy các điểm \(D,\,\,C\) trên các đường đó sao cho \(AD = BC = 4{\rm{\;cm}}\) (Hình k và Hình l). Nối \(C\) với \(D\) ta được hình vuông \(ABCD\) có cạnh 4 cm như đã cho (Hình m). Do đó ý d) là khẳng định đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
1) a) \(39 - 125:\left[ {\left( {{5^{11}} \cdot 16 + 9 \cdot {5^{11}}} \right):{5^{12}}} \right]\) \( = 39 - 125:\left[ {{5^{11}} \cdot \left( {16 + 9} \right):{5^{12}}} \right]\) \( = 39 - 125:\left[ {{5^{11}} \cdot 25:{5^{12}}} \right]\) \( = 39 - 125:\left[ {{5^{11}} \cdot {5^2}:{5^{12}}} \right]\) \[ = 39 - {5^3}:{5^{11 + 2 - 12}}\] \[ = 39 - {5^3}:{5^1}\] \[ = 39 - {5^2}\] \[ = 39 - 25 = 14.\] |
b) \[2 \cdot 53 \cdot 12 + 4 \cdot 6 \cdot 87 - 3 \cdot 8 \cdot 40\] \[ = 24 \cdot 53 + 24 \cdot 87 - 24 \cdot 40\] \[ = 24 \cdot \left( {53 + 87 - 40} \right)\] \[ = 24 \cdot 100\] \[ = 2\,\,400.\]
|
2) \(121 + \left( {5x - 21} \right):4 = 127\)
\(\left( {5x - 21} \right):4 = 127 - 121\)
\(\left( {5x - 21} \right):4 = 6\)
\(5x - 21 = 6 \cdot 4\)
\(5x - 21 = 24\)
\(5x = 24 + 21\)
\(5x = 45\)
\(x = 45:5\)
\(x = 9.\)
Vậy \(x = 9.\)
Lời giải
Hướng dẫn giải
Chia các vé xổ số thành hai loại: các vé dạng \[\overline {abcabc} \] và các vé dạng \(\overline {abcdef} \) mà \(\overline {abc} \ne \overline {def} \) (ví dụ 812650).
⦁ Xét vé thuộc dạng \[\overline {abcabc} .\]
Ta có: \[\overline {abcabc} = \overline {abc000} + \overline {abc} = \overline {abc} \cdot 1000 + \overline {abc} = \overline {abc} \cdot 1001 = \overline {abc} \cdot 7 \cdot 11 \cdot 13.\]
Do đó, mỗi vé thuộc dạng thứ nhất đều chia hết cho 13 nên tổng các số của vé dạng này cũng chia hết cho 13. (1)
⦁ Ghép hai vé thuộc dạng thứ hai là \(\overline {abcdef} \) và \(\overline {defabc} \) thành một cặp, tổng hai số này là:
\[\overline {abcdef} + \overline {defabc} = \overline {abc} \cdot 1000 + \overline {def} + \overline {def} \cdot 1000 + \overline {abc} \]
\[ = 1001 \cdot \overline {abc} + 1001 \cdot \overline {def} = 1001 \cdot \left( {\overline {abc} + \overline {def} } \right) = 7 \cdot 11 \cdot 13 \cdot \left( {\overline {abc} + \overline {def} } \right)\,\,\, \vdots \,\,\,13.\]
Như vậy, tổng các số của vé dạng thứ hai này cũng chia hết cho 13. (2)
Từ (1) và (2) ta có tổng tất cả các số ghi trên vé xổ số có sáu chữ số mà tổng ba chữ số đầu bằng tổng ba chữ số cuối thì chia hết cho 13 (các chữ số đầu có thể bằng 0).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.