Câu hỏi:
06/06/2025 39
Cho hình vuông \(ABCD\) có cạnh bằng 4 cm. Khi đó
a) \(AB = BC = CD = DA = 4{\rm{\;cm}}.\)
b) \(AC\) và \(BD\) song song với nhau.
c) Mỗi góc ở các đỉnh của hình vuông bằng nhau và bằng \(60^\circ .\)
d) Vẽ cạnh \(AB = 4{\rm{\;cm}}{\rm{.}}\) Dùng thước eke vẽ các đường vuông góc với \(AB\) tại \(A,\,\,B,\) sau đó lần lượt lấy các điểm \(D,\,\,C\) trên các đường đó sao cho \(AD = BC = 4{\rm{\;cm}}.\) Nối \(C\) với \(D\) ta được hình vuông \(ABCD\) có cạnh 4 cm như đã cho.
Cho hình vuông \(ABCD\) có cạnh bằng 4 cm. Khi đó
a) \(AB = BC = CD = DA = 4{\rm{\;cm}}.\)
b) \(AC\) và \(BD\) song song với nhau.
c) Mỗi góc ở các đỉnh của hình vuông bằng nhau và bằng \(60^\circ .\)
d) Vẽ cạnh \(AB = 4{\rm{\;cm}}{\rm{.}}\) Dùng thước eke vẽ các đường vuông góc với \(AB\) tại \(A,\,\,B,\) sau đó lần lượt lấy các điểm \(D,\,\,C\) trên các đường đó sao cho \(AD = BC = 4{\rm{\;cm}}.\) Nối \(C\) với \(D\) ta được hình vuông \(ABCD\) có cạnh 4 cm như đã cho.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: a) Đúng. b) Sai. c) Sai. d) Đúng.
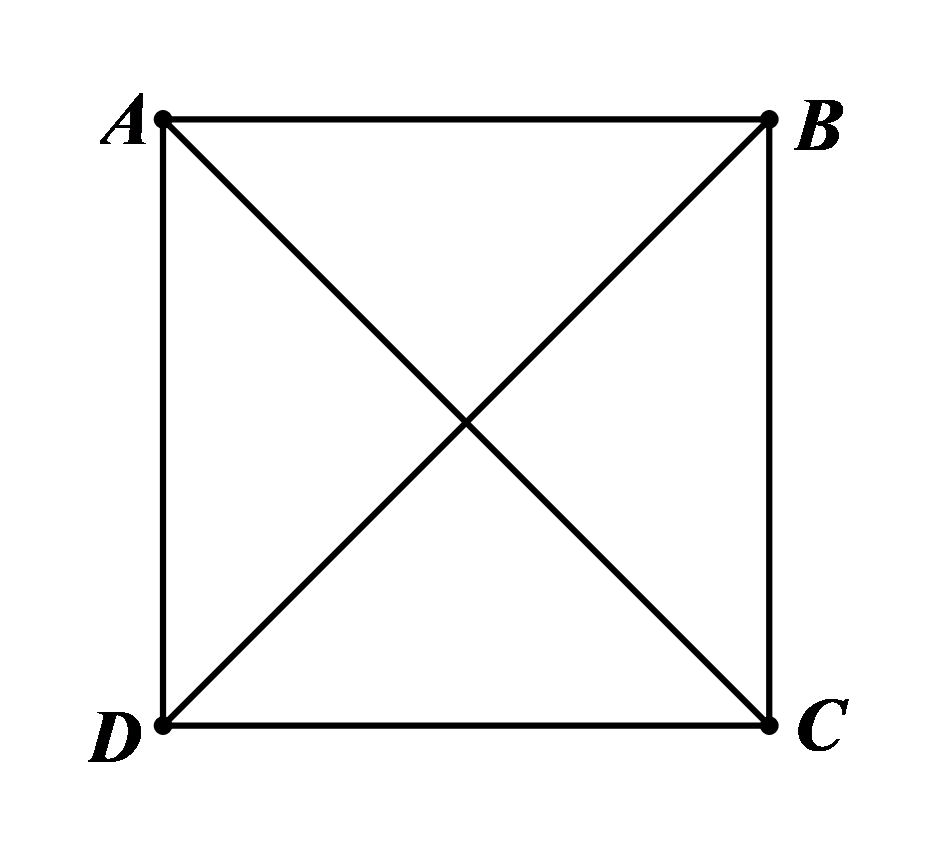
⦁ Hình vuông \(ABCD\) có cạnh bằng 4 cm nên \(AB = BC = CD = DA = 4{\rm{\;cm}}.\) Do đó ý a) là khẳng định đúng.
⦁ Hình vuông \(ABCD\) có \(AC\) và \(BD\) là hai đường chéo nên không song song với nhau mà cắt nhau. Do đó ý b) là khẳng định sai.
⦁ Hình vuông \(ABCD\) có mỗi góc ở các đỉnh của hình vuông bằng nhau và bằng \(90^\circ .\) Do đó ý c) là khẳng định đúng.
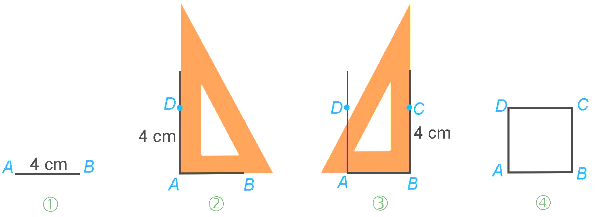
⦁ Vẽ cạnh \(AB = 4{\rm{\;cm}}\) (Hình j). Dùng thước eke vẽ các đường vuông góc với \(AB\) tại \(A,\,\,B,\) sau đó lần lượt lấy các điểm \(D,\,\,C\) trên các đường đó sao cho \(AD = BC = 4{\rm{\;cm}}\) (Hình k và Hình l). Nối \(C\) với \(D\) ta được hình vuông \(ABCD\) có cạnh 4 cm như đã cho (Hình m). Do đó ý d) là khẳng định đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
1) a) \(39 - 125:\left[ {\left( {{5^{11}} \cdot 16 + 9 \cdot {5^{11}}} \right):{5^{12}}} \right]\) \( = 39 - 125:\left[ {{5^{11}} \cdot \left( {16 + 9} \right):{5^{12}}} \right]\) \( = 39 - 125:\left[ {{5^{11}} \cdot 25:{5^{12}}} \right]\) \( = 39 - 125:\left[ {{5^{11}} \cdot {5^2}:{5^{12}}} \right]\) \[ = 39 - {5^3}:{5^{11 + 2 - 12}}\] \[ = 39 - {5^3}:{5^1}\] \[ = 39 - {5^2}\] \[ = 39 - 25 = 14.\] |
b) \(57 \cdot 34 + 100 \cdot 43 + 57 \cdot 66\) \( = \left( {57 \cdot 34 + 57 \cdot 66} \right) + 100 \cdot 43\) \( = 57 \cdot \left( {34 + 66} \right) + 100 \cdot 43\) \( = 57 \cdot 100 + 100 \cdot 43\) \( = 100 \cdot \left( {57 + 43} \right)\) \( = 100 \cdot 100\) \( = 10\,\,000.\) |
2) \(121 + \left( {5x - 21} \right):4 = 127\)
\(\left( {5x - 21} \right):4 = 127 - 121\)
\(\left( {5x - 21} \right):4 = 6\)
\(5x - 21 = 6 \cdot 4\)
\(5x - 21 = 24\)
\(5x = 24 + 21\)
\(5x = 45\)
\(x = 45:5\)
\(x = 9.\)
Vậy \(x = 9.\)
Lời giải
Hướng dẫn giải
Xét biểu thức \(A = 2 + {21^{23}} + {25^{125}}.\)
Ta có \({21^{23}}\) có chữ số tận cùng là 1 (vì \[{\left( {\overline {...1} } \right)^n} = \overline {...1} ).\]
\({25^{125}}\) có chữ số tận cùng là 5 (vì \[{\left( {\overline {...5} } \right)^n} = \overline {...5} ).\]
Khi đó, \(A = 2 + {21^{23}} + {25^{125}}\) có chữ số tận cùng là: \(2 + 1 + 5 = 8\) (có dạng \(\overline {...8} )\) nên \(A\,\, \vdots \,\,2.\)
Mà \(A = 2 + {21^{23}} + {25^{125}} > 1\) và có nhiều hơn 2 ước nên \(A\) là hợp số.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo