Câu hỏi:
19/06/2025 8
1. Một viên bi lăn từ vị trí \(A\) đến vị trí \(D\) theo đường gấp khúc \(ABCD\) hết 21 giây, biết rằng \(AB = 10{\rm{\;cm}},\) \(BC = 12{\rm{\;cm}},\) \(CD = 6{\rm{\;cm}}\) (hình vẽ bên). Hỏi nếu viên bi đó lăn theo đoạn thẳng \(AD\) thì hết bao nhiêu giây? Giả sử vận tốc của viên bi không thay đổi.
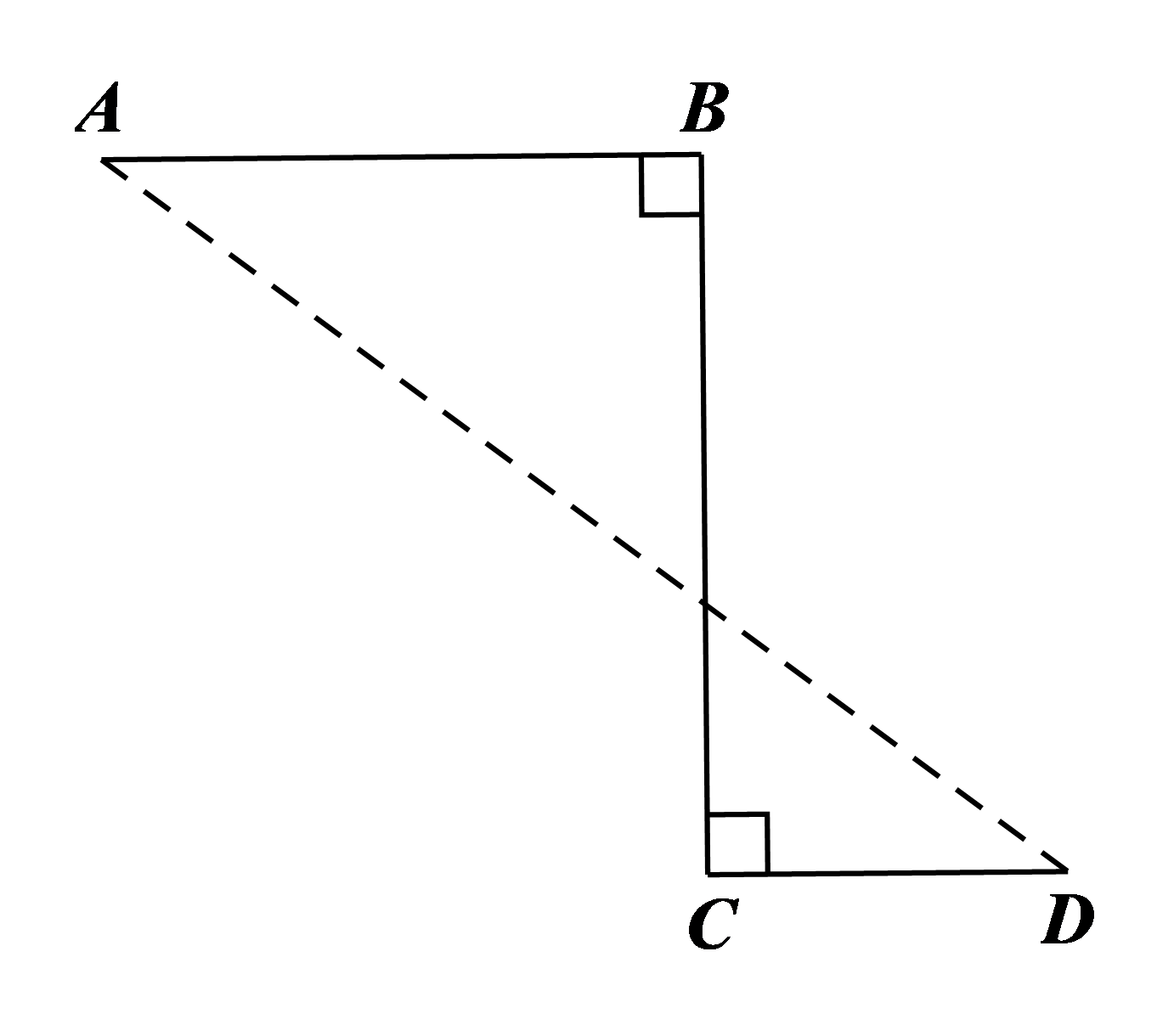
2. Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m}}{\rm{,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm}}{\rm{,}}\)chiều cao \(90{\rm{ cm}}\). Đỉnh Fansipan được minh họa bằng bởi hình chóp tam giác đều \(S.ABC\). Đường cao của mặt đáy là \(CH\,;\,\,G\) là trọng tâm của mặt đáy (như hình vẽ).
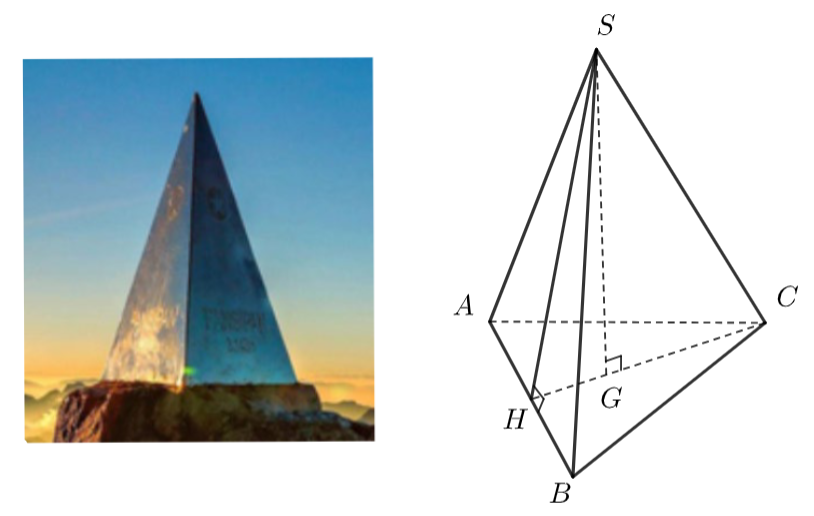
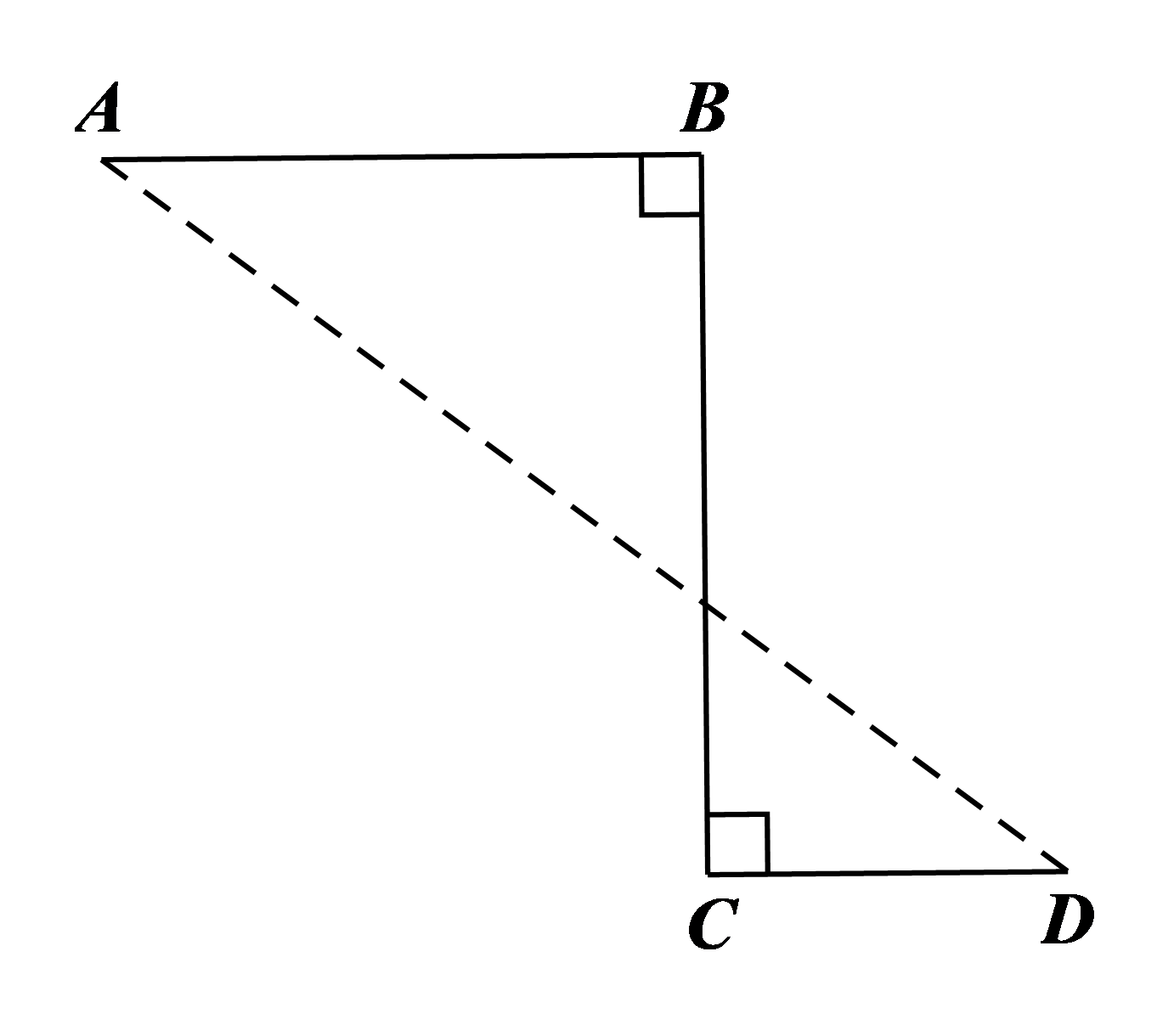
2. Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m}}{\rm{,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm}}{\rm{,}}\)chiều cao \(90{\rm{ cm}}\). Đỉnh Fansipan được minh họa bằng bởi hình chóp tam giác đều \(S.ABC\). Đường cao của mặt đáy là \(CH\,;\,\,G\) là trọng tâm của mặt đáy (như hình vẽ).
Quảng cáo
Trả lời:
Giải bởi Vietjack
1.
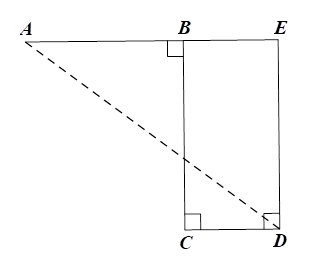
Từ \(D\) vẽ \(Dx \bot CD\) cắt tia \(AB\) tại \(E.\)
Xét tứ giác \(BCDE\) có \(\widehat {BCD} = \widehat {CDE} = \widehat {CBE} = 90^\circ \) nên \(BCDE\) là hình chữ nhật.
Do đó \(DE = BC = 12{\rm{\;cm}},\,\,BE = CD = 6{\rm{\;cm}}.\)
Có \(AE = AB + BE = 10 + 6 = 16{\rm{\;}}\left( {{\rm{cm}}} \right).\)
Áp dụng định lí Pythagore cho \(\Delta ADE\) vuông tại \(E,\) ta được: \(A{D^2} = A{E^2} + D{E^2} = {16^2} + {12^2} = 400.\)
Suy ra \[AD = \sqrt {400} = 20{\rm{\;}}\left( {{\rm{cm}}} \right).\]Thời gian viên bi lăn theo đoạn thẳng \(AD\) là \(\frac{{20 \cdot 21}}{{28}} = 15\) (giây).
2. a) Mặt đáy của hình chóp \(S.ABC\) là một tam giác đều \(ABC\) có cạnh \(60{\rm{ cm}}{\rm{.}}\)
Tam giác đều \(ABC\) có \(CH\)là đường cao nên \(CH\) cũng là đường trung tuyến nên
\(HA = HB = \frac{{AB}}{2} = 30{\rm{ }}\left( {{\rm{cm}}} \right){\rm{.}}\)
Áp dụng định lý Pythagore vào \(\Delta BHC\) vuông tại \(H\), ta có:
\(B{C^2} = H{B^2} + H{C^2}\) suy ra \[H{C^2} = B{C^2} - H{B^2} = {60^2} - {30^2} = 2{\rm{ }}700\].
Do đó \(CH = \sqrt {2700} = 30\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).
Vậy \(HA = 30{\rm{ cm}}\,;\,\,CH = 30\sqrt 3 {\rm{ cm}}.\)
b) Gọi \(G\) là trọng tâm của mặt đáy nên \(GH = \frac{1}{3}HC = \frac{{30\sqrt 3 }}{3} = 10\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).
Hình chóp \(S.ABC\) có đường cao \(SG\) nên \(SG \bot HC.\)
Áp dụng định lý Pythagore vào \(\Delta SHG\) vuông tại \(G\), ta có:
\(S{H^2} = S{G^2} + H{G^2} = {90^2} + {30^2} = 9\,\,000\).
Suy ra \(SH = \sqrt {9\,\,000} = 30\sqrt {10} {\rm{ }}\left( {{\rm{cm}}} \right){\rm{.}}\)
Nửa chu vi đáy là: \(P = \frac{1}{2}\left( {60 + 60 + 60} \right) = 90{\rm{ }}\left( {{\rm{cm}}} \right)\).
Diện tích xung quanh của hình chóp là \(S = P \cdot d = 90 \cdot 30\sqrt {10} \approx 8\,\,538{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Vậy diện tích xung quanh của hình chóp là \(8\,\,538{\rm{ c}}{{\rm{m}}^{\rm{2}}}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: a) Đúng. b) Đúng. c) Sai. d) Sai.
⦁ Mỗi hộp quà có 5 mặt gồm 4 mặt bên và 1 mặt đáy. Do đó ý a) đúng.
⦁ Diện tích xung quanh của một hộp quà là: \({S_{xq}} = \frac{1}{2} \cdot \left( {4 \cdot 6} \right) \cdot 4 = 48{\rm{\;}}\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\) Do đó ý b) đúng.
⦁ Diện tích các mặt của hộp quà là: Do đó ý c) sai.
⦁ Để làm 4 hộp quà bạn Uyên cần dùng diện tích giấy là: \(4 \cdot 84 = 336{\rm{\;}}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\) Do đó ý d) sai.
Lời giải
Đáp số: 27.
Thể tích khúc gỗ hình lập phương là: \[{30^3} = 27\,\,000\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\]
Thể tích của phần gỗ còn lại hình chóp tứ giác đều là:
\(\frac{1}{3} \cdot {30^2} \cdot 30 = 9\,\,000\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Thể tích của khối gỗ bị cắt đi là:
\[27\,\,000 - 9\,\,000 = 18\,\,000\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right) = 18\,\,\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right).\]
Vậy thể tích của phần gỗ bị cắt đi là \[18\,\,{\rm{d}}{{\rm{m}}^{\rm{3}}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án
-
Dạng 2: Bài luyện tập 1 Dạng 2: Rút gọn phân thức có đáp án
Nhắn tin Zalo