Câu hỏi:
19/06/2025 6
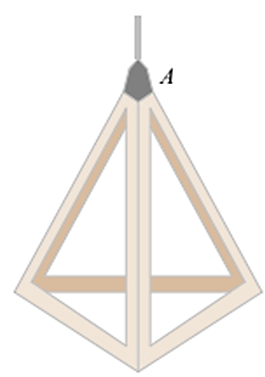
Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?
![Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid6-1750304278.png)
Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là \[20{\rm{ cm}}.\]
a) Tính độ dài trung đoạn của hình chóp.
b) Tính diện tích xung quanh của chiếc đèn.
c) Bạn Nam đọc và thấy rằng khi treo đèn thì khoảng cách từ đáy của đèn cách mặt trền là \[1{\rm{ m}}\] là tốt nhất. Vậy bạn Nam cần đưa đoạn dây điện từ đầu đèn (vị trí \(A)\) tới mặt trần là bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?
Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là \[20{\rm{ cm}}.\]
a) Tính độ dài trung đoạn của hình chóp.
b) Tính diện tích xung quanh của chiếc đèn.
c) Bạn Nam đọc và thấy rằng khi treo đèn thì khoảng cách từ đáy của đèn cách mặt trền là \[1{\rm{ m}}\] là tốt nhất. Vậy bạn Nam cần đưa đoạn dây điện từ đầu đèn (vị trí \(A)\) tới mặt trần là bao nhiêu (làm tròn kết quả đến hàng phần mười)?Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Áp dụng định lí Pythagore cho các tam giác vuông \(AMO,\,\,ONC,\,\,OMD,\,\,OBE,\) ta tính được:
⦁ \(O{A^2} = {3^2} + {4^2} = 25\) hay \(OA = 5{\rm{\;m;}}\)
⦁ \(O{C^2} = {6^2} + {8^2} = 100\) hay \(OC = 10{\rm{\;m}};\)
⦁ \(O{D^2} = {3^2} + {8^2} = 73\) hay \(OD = \sqrt {73} {\rm{\;m}};\)
⦁ \(O{B^2} = {4^2} + {6^2} = 52\) hay \(OB = \sqrt {52} {\rm{\;m}}{\rm{.}}\)
Vì \[OA = 5{\rm{\;m}} < 9{\rm{\;m}},\,\,OD = \sqrt {73} {\rm{\;m}} < 9{\rm{\;m}},\,\,OB = \sqrt {52} {\rm{\;m}} < 9{\rm{\;m}},\,\,OC = 10{\rm{\;m}} > 9{\rm{\;m}}{\rm{,}}\] nên chú cún có thể đến các vị trí \(A,\,\,D,\,\,B\) nhưng không thể đến được vị trí \(C.\)2. a) Chiếc đèn được mô phỏng thành hình chóp tam giác đều \(A.BCD\) như hình vẽ. Gọi \(AH\) là trung đoạn kẻ từ đỉnh \(A\) của hình chóp.
Theo bài ta có: \(AB = AC = AD = 20\,\,{\rm{cm;}}\)
\[BC = CD = DB = 20\,\,{\rm{cm}}.\]
\(\Delta ACD\) đều nên \(AH\) vừa là đường cao vừa là đường trung tuyến.
Do đó \(DH = CH = \frac{1}{2}CD = 10\) cm.
Xét \(\Delta AHC\) vuông tại \(H\), theo định lí Pythagore ta có: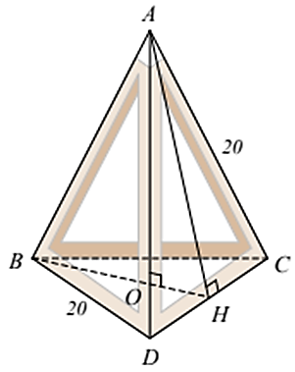
\(A{H^2} = A{C^2} - C{H^2} = {20^2} - {10^2} = 300\)
Suy ra \[AH = \sqrt {300} = \sqrt {100.3} = \sqrt {{{\left( {10\sqrt 3 } \right)}^2}} = 10\sqrt 3 \,\,\left( {{\rm{cm}}} \right).\]
b) Chu vi đáy của hình chóp là: \[C = 3BD = 3 \cdot 20 = 60\,\,\left( {{\rm{cm}}} \right).\]
Diện tích xung quanh của chiếc đèn là:
\[{S_{xq}} = \frac{1}{2}C \cdot AH = \frac{1}{2} \cdot 60 \cdot 10\sqrt 3 = 300\sqrt 3 \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right).\]
c) Vì \(\Delta ADC\) và \(\Delta BDC\) đều là các tam giác đều có cạnh 20 cm nên hai đường cao \(AH\) và \(BH\) của hai tam giác bằng nhau.
Vì \(O\) là trọng tâm \(\Delta BDC\) nên \(OH = \frac{1}{3}BH = \frac{{10\sqrt 3 }}{3}\,\,\left( {{\rm{cm}}} \right).\)
\(\Delta AOH\)vuông tại \(O\), theo định lí Pythagore, ta có:
\(A{O^2} = A{H^2} - O{H^2} = 300 - {\left( {\frac{{10\sqrt 3 }}{3}} \right)^2} = 300 - \frac{{300}}{9} = \frac{{800}}{3}\).
Suy ra \(AO = \sqrt {\frac{{800}}{3}} \approx 16,3\,\,\left( {{\rm{cm}}} \right).\)
Khi đó bạn Nam cần đưa dây diện từ đầu đèn tới trần nhà khoảng là \(100 - 16,3 = 83,7\,\,\left( {{\rm{cm}}} \right).\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: 5.
Ta có \[V = \frac{1}{3}S \cdot h\] nên \[S = \frac{{3V}}{h} = \frac{{3 \cdot 50}}{9} = 25{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\].
Vì đáy của hình chóp tứ giác đều cạnh a là hình vuông nên độ dài cạnh đáy là \[a = \sqrt {25} = 5{\rm{ }}\left( {{\rm{cm}}} \right)\].
Vậy độ dài cạnh đáy của hình chóp đó là \({\rm{5}}\;{\rm{cm}}\).
Lời giải
Đáp án đúng là: C
Hình chóp tam giác đều \(S.ABC\) có mặt bên là các tam giác cân nên \(\Delta SBC\) là tam giác cân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án
-
Dạng 2: Bài luyện tập 1 Dạng 2: Rút gọn phân thức có đáp án
Nhắn tin Zalo