Hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Một cửa hàng có \(69\frac{3}{5}{\rm{ kg}}\) gạo. buổi sáng bán được \(15\frac{1}{5}{\rm{ kg}}\) dạo. buổi chiều bán được số gạo gấp \(3\) lần buổi sáng. Hỏi sau cả hai buổi cửa hàng còn lại bao nhiêu kilogram gạo?
Trả lời:
Hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Một cửa hàng có \(69\frac{3}{5}{\rm{ kg}}\) gạo. buổi sáng bán được \(15\frac{1}{5}{\rm{ kg}}\) dạo. buổi chiều bán được số gạo gấp \(3\) lần buổi sáng. Hỏi sau cả hai buổi cửa hàng còn lại bao nhiêu kilogram gạo?
Trả lời:
Quảng cáo
Trả lời:
Đáp án: \(24\)
Ta có: \(15\frac{1}{5}{\rm{ kg}} = \frac{{76}}{5}{\rm{ kg}}\); \(69\frac{3}{5}{\rm{ kg}} = \frac{{348}}{5}{\rm{ kg}}\)
Buổi chiều cửa hàng bán được số kilogram gạo là: \(\frac{{76}}{5}.3 = \frac{{228}}{5}{\rm{ }}\left( {{\rm{kg}}} \right)\).
Sau cả hai buổi cửa hàng còn lại số kilogram gạo là: \(\frac{{348}}{5} - \frac{{228}}{5} = \frac{{120}}{5} = 24{\rm{ }}\left( {{\rm{kg}}} \right)\).
Vậy sau cả hai buổi cửa hàng còn lại \(24{\rm{ kg}}\) gạo.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đặt \(A = \frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{70}}\)
Ta có: \(A = \frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{30}} + \frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{50}} + \frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{70}}\)
\(A = \left( {\frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{30}}} \right) + \left( {\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{50}}} \right) + \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{70}}} \right)\)
Nhận thấy \(\frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{30}} > \frac{1}{{30}} + \frac{1}{{30}} + .... + \frac{1}{{30}}\) hay \(\frac{1}{{11}} + \frac{1}{{12}} + \frac{1}{{13}} + ... + \frac{1}{{30}} > \frac{1}{{30}}.20 = \frac{2}{3}\)
\(\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{50}} > \frac{1}{{50}} + \frac{1}{{50}} + .... + \frac{1}{{50}}\) hay \(\frac{1}{{31}} + \frac{1}{{32}} + ... + \frac{1}{{50}} > \frac{1}{{50}}.20 = \frac{2}{5}\).
\(\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{70}} > \frac{1}{{70}} + \frac{1}{{70}} + .... + \frac{1}{{70}}\) hay \(\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{70}} > \frac{1}{{70}}.20 = \frac{2}{7}\).
Do đó, \(A > \frac{2}{3} + \frac{2}{5} + \frac{2}{7}\) hay \(A > \frac{{142}}{{105}} > \frac{{140}}{{105}} = \frac{4}{3}\).
Vậy \(A > \frac{4}{3}\) (đpcm)
Câu 2
A. \(\frac{{17}}{{13}}.\)
Lời giải
Đáp án đúng là: B
Số đối của phân số \(\frac{{13}}{{17}}\) là \(\frac{{ - 13}}{{17}}.\) \(\frac{3}{{15}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
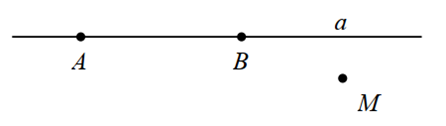
A. Điểm \(M\) thuộc đường thẳng \(a.\)
B. Điểm \(A\) thuộc đường thẳng \(a.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. luôn nhỏ hơn \(1.\)
B. luôn lớn hơn \(1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{1}{5}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.