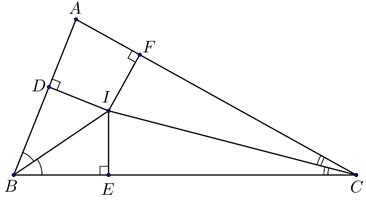
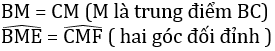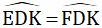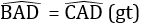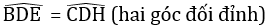Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Vẽ ID ⊥ AB (D ∈ AB), IE ⊥ BC (E ∈ BC), IF ⊥ CA (F ∈ CA). Chứng minh ID = IE = IF.

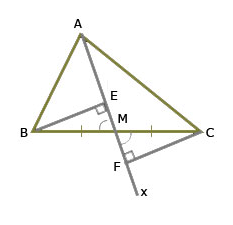
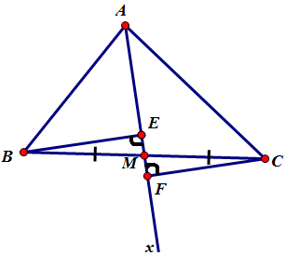
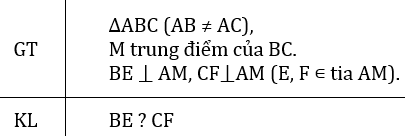
Hai tam giác vuông BME và CMF có

⇒ ΔBME = ΔCMF (cạnh huyền – góc nhọn)

⇒ BE = CF (hai cạnh tương ứng).

* Chú ý: Các em có thể suy nghĩ tại sao cần điều kiện AB ≠ AC ???

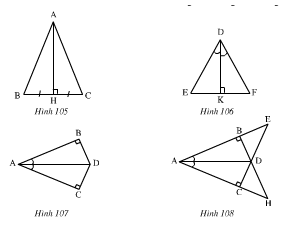
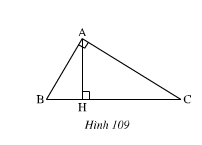
+ Hình 105: ΔABH và ΔACH cùng vuông tại H có:

      BH = CH (gt)

      AH cạnh chung

      ⇒ ΔABH = ΔACH (hai cạnh góc vuông)

+ Hình 106: Xét ΔDKE vuông tại K và ΔDKF vuông tại K có:

      DK chung

      ⇒ ΔDKE và ΔDKF (cạnh góc vuông – góc nhọn kề).

+ Hình 107: Xét ΔABD vuông tại B và ΔACD vuông tại C có:

      AD chung

      ⇒ ΔABD = ΔACD (cạnh huyền – góc nhọn )

+ Hình 108:

      • ΔABD = ΔACD (cạnh huyền – góc nhọn) (giống hình 107).

      ⇒ AB = AC và BD = CD (hai cạnh tương ứng)

      • Xét ΔABH vuông tại B và ΔACE vuông tại C có

      Góc A chung

      AB = AC

      ⇒ΔABH = ΔACE (cạnh góc vuông – góc nhọn kề).

      • Xét ΔDBE vuông tại B và ΔDCH vuông tại C có:

      BD = DC (chứng minh trên)

      ⇒ ΔDBE = ΔDCH (cạnh góc vuông – góc nhọn kề)