(1,5 điểm) Bạn An biểu diễn được số cây trồng được của các lớp 6 trong một trường THCS nhân dịp lễ trồng cây xanh như biểu đồ sau:
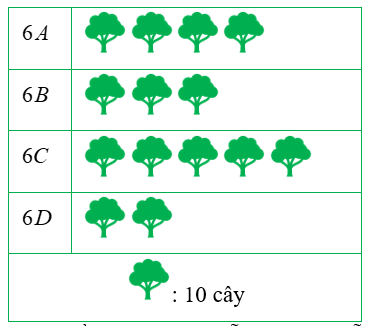
a) Lập bảng thống kê số cây xanh trồng được của mỗi lớp theo mẫu sau:
b) Cả bốn lớp trồng được bao nhiêu cây?
c) Chênh lệch số cây trồng được giữa lớp trồng được nhiều nhất và ít nhất là bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Số cây xanh lớp \(6A\) trồng được là: \(4 \cdot 10 = 40\) (cây).
Số cây xanh lớp \(6B\) trồng được là: \(3 \cdot 10 = 30\) (cây).
Số cây xanh lớp \(6C\) trồng được là: \(5 \cdot 10 = 50\) (cây).
Số cây xanh lớp \(6D\) trồng được là: \(2 \cdot 10 = 20\) (cây).
Ta lập được bảng thống kê số cây xanh trồng được của mỗi lớp như sau:
|
Lớp |
\(6A\) |
\(6B\) |
\(6C\) |
\(6D\) |
|
Số cây xanh |
40 |
30 |
50 |
20 |
b) Tổng số cây xanh trồng được của bốn lớp \(6A,6B,6C,6D\) là:
\(40 + 30 + 50 + 20 = 140\) (cây).
c) Lớp \(6C\) trồng được nhiều nhất, lớp \(6D\) trồng được ít nhất.
Lớp \(6C\) trồng được nhiều hơn lớp \(6D\) số cây là:
\(50 - 20 = 30\) (cây).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
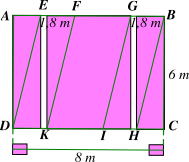
a) Các hình tam giác là: \(ADE,\,\,BCH.\)
Các hình hình hành là: \[EFKD,\,\,GBHI,\,\,FHIK.\]
b) Hai hình bình hành \[EFKD\] và \[GBHI\] có kích thước bằng nhau nên diện tích hình bình hành \[EFKD\] và diện tích hình bình hành \[GBHI\] bằng nhau.
Diện tích trồng hoa là: \[2 \cdot \left( {1,8 \cdot 6} \right) = 21,6{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
c) Diện tích mảnh đất là: \(8 \cdot 6 = 48{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích trồng cỏ là: \(48 - 21,6 = 26,4{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Tiền công trả cho trồng hoa là:
\(80\,\,000 \cdot 21,6 = 1\,\,728\,\,000\) (đồng).
Tiền công trả cho trồng cỏ là:
\(60\,\,000 \cdot 26,4 = 1\,\,584\,\,000\) (đồng).
Tiền công cần chi trả cho trồng cả hoa và cỏ là:
\(1\,\,728\,\,000 + 1\,\,584\,\,000 = 3\,\,312\,\,000\) (đồng).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) \(2x + {2^0} = {3^5}:{3^3}\) \(2x + 1 = {3^2}\) \(2x + 1 = 9\) \(2x = 8\) \(x = 4\). Vậy \(x = 4.\) b) \(99 - \left( {5 - 3x} \right) = - 2\) \(5 - 3x = 99 - \left( { - 2} \right)\) \(5 - 3x = 101\) \(3x = 5 - 101\) \(3x = - 96\) \(x = - 32\) Vậy \(x = - 32\). |
c) \(2{\left( {x - 6} \right)^2} - 1 = 49\) \(2{\left( {x - 6} \right)^2} = 50\) \({\left( {x - 6} \right)^2} = 25\) |
|
|
Trường hợp 1: \(x - 6 = 5\) \(x = 11\) Vậy \(x \in \left\{ {11;\,\,1} \right\}\). |
Trường hợp 2: \(x - 6 = - 5\) \(x = 1\) |
|
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
(2,5 điểm)
1. Báo cáo kinh doanh trong 6 tháng đầu năm của công ty A được thống kê như sau:
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
|
Lợi nhuận (triệu đồng) |
\(500\) |
\( - 105\) |
\(539\) |
\(385\) |
\( - 34\) |
\( - 13\) |
Hỏi trung bình mỗi tháng công ty A lãi hay lỗ bao nhiêu tiền?
2. Một tờ bìa hình chữ nhật có chiều dài \(120\,\,{\rm{cm}}\), chiều rộng \(90\,\,{\rm{cm}}\). Người ta muốn cắt tờ bìa hình chữ nhật thành những hình vuông bằng nhau. Tính độ dài lớn nhất của cạnh mỗi hình vuông cắt ra và số tờ bìa hình vuông cắt được.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập