1) Mỗi tháng các bạn học sinh lớp 6 thường được phụ huynh và cô giáo tổ chức sinh nhật cùng với cả lớp. Biểu đồ cột kép sau đây thống kê số miếng bánh ngọt trong 3 tháng liên tiếp của 2 lớp 6A và 6B đã dùng trong bữa tiệc sinh nhật.

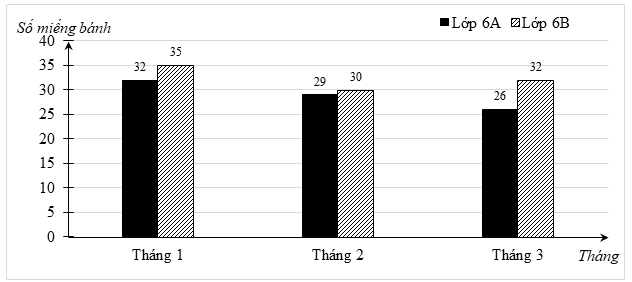
         a) Trong ba tháng đầu tiên, số học sinh dùng hết số bánh ở mỗi buổi nhiều nhất là bao nhiêu? Ít nhất là bao nhiêu?

         b) So sánh số học sinh dùng bánh ngọt trong mỗi bữa tiệc sinh nhật ở hai lớp. Em có thể đưa ra một giải thích hợp lí cho điều này được không?

         c) Để tránh lãng phí trong những bữa tiệc tiếp theo, em hãy chọn phương án phù hợp nhất đối với việc chuẩn bị bánh cho học sinh của cả 2 lớp:

         j 35 miếng bánh.                                              k 40 miếng bánh.

         l 45 miếng bánh.                                              m 50 miếng bánh.

     2) Hai bạn Dũng và Nam chơi 1 ván oẳn tù tì gồm 10 lần theo luật chơi: Búa (B) thắng Kéo (K); Kéo (K) thắng Lá (L), Lá (L) thắng Búa (B) và hòa nhau nếu cùng loại.

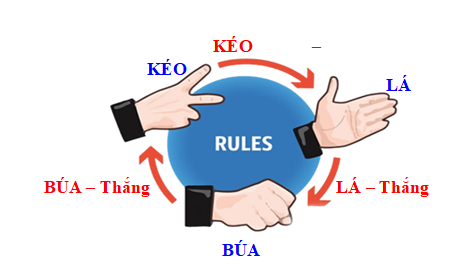
     Sau đây là kết quả của mỗi ván chơi:

Lần thứ	1	2	3	4	5	6	7	8	9	10
Dũng	L	B	B	K	L	B	K	B	K	K
Nam	B	K	L	L	K	B	L	K	L	B

     Tính xác suất thực nghiệm của sự kiện “Dũng không thua Nam”.

Tìm \(x,\) biết:

a) \(x - \frac{5}{6} = \frac{{ - 7}}{6}.\)                              

b) \[x + 1,05 = 0,2 - 4,25.\]        

c) \[\left( {5 - 4x} \right)\left( {\frac{5}{4}x - 2} \right) = 0.\]

Một người bán cam, buổi sáng bán được \(60\% \) số cam mang đi, buổi chiều bán được \(\frac{{13}}{{18}}\) số cam còn lại. Lúc về, người đó còn 20 quả cam.

a) Hỏi số cam người đó mang đi bán là bao nhiêu?

b) Tính tỉ số phần trăm số cam người đó bán được buổi sáng so với tổng số cam bán được trong ngày.

Lần thứ nhất bác bán được \[\frac{1}{6}\] số quýt và 2 quả.

Lần thứ hai bác bán được \[\frac{1}{6}\] số quýt còn lại và 4 quả.

Lần thứ ba bác bán được \[\frac{1}{6}\] số quýt còn lại sau hai lần bán và 6 quả.

Lần thứ tư bác bán được \[\frac{1}{6}\] số quýt còn lại sau ba lần bán và 8 quả.

Lần thứ năm bác bán được \[\frac{1}{6}\] số quýt còn lại sau bốn lần bán và 10 quả cuối cùng.

Tính số quýt bác nông dân đã bán.

     1) Cho đoạn thẳng \(AB\) có độ dài \({\rm{8}}\,\,{\rm{cm}}{\rm{.}}\) Trên đoạn thẳng \(AB\) lấy hai điểm \(M\) và \(N\) sao cho \(AM = MN = 2\,{\rm{cm}}\) (điểm \(N\) không nằm giữa hai điểm \(A\) và \(M).\)

a) Tính độ dài đoạn thẳng \(MB.\)

b) Điểm \(N\) có phải là trung điểm đoạn thẳng \[AB\] không? Vì sao?

c) Vẽ điểm \(P\) là trung điểm của đoạn thẳng \(NB.\) Tính \(AP\) và \(MP.\)

     2) Ta có thể xem kim phút và kim giờ của đồng hồ là hai tia chung gốc (gốc trùng với trục quay của hai kim). Tại mỗi thời điểm hai kim tạo thành một góc.

         a) Biết rằng khi kim giờ và kim phút thay nhau chỉ số 12 và số 6 thì tạo thành một góc có số đo là \(180^\circ .\) Vậy khi hai kim lần lượt chỉ hai số cạnh nhau thì tạo thành một góc có số đo là bao nhiêu độ?

         b) Góc tạo bởi kim phút và kim giờ lúc 2 giờ 30 phút có số đo là bao nhiêu độ?

Thực hiện phép tính (tính hợp lí nếu có thể):

a) \(\frac{2}{5} - \frac{1}{5} \cdot \frac{3}{{ - 4}}.\)                          

b) \(\left( { - 12,5} \right) + 17,55 + \left( { - 3,5} \right) - \left( { - 2,45} \right).\)

c) \(\frac{{ - 3}}{5}:\frac{7}{5} - \frac{3}{5}:\frac{7}{5} + 2\frac{3}{5}.\)

d) \[1\frac{{13}}{{15}} \cdot {\left( {0,5} \right)^2} \cdot 3 + \left( {40\% - 1\frac{{19}}{{60}}} \right):1\frac{7}{8}.\]