a) Trong các chữ cái sau, chữ cái nào có nhiều hơn một trục đối xứng?

G I A P H O N V Đ C L P

b) Trong các hình sau: hình vuông, hình tam giác đều, hình lục giác đều, hình bình hành, hình chữ nhật, hình thoi, hình thang cân, những hình nào là hình vừa có trục đối xứng vừa có tâm đối xứng?

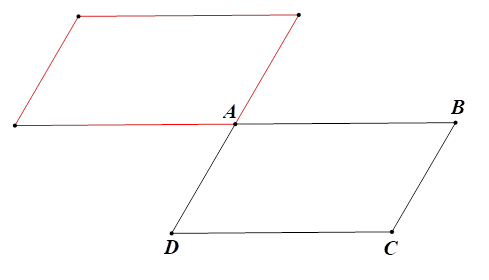
c) Cho hình bình hành \(ABCD.\) Vẽ hình đối xứng qua tâm là đỉnh \(A\) của hình bình hành \(ABCD.\)

Thực hiện phép tính (tính hợp lí nếu có thể):

a) \[\frac{7}{{30}} + \frac{{ - 12}}{{37}} + \frac{{23}}{{30}} + \frac{{ - 25}}{{37}}.\]                                                             

b) \(\left( { - 0,4} \right) \cdot \left( { - 0,5} \right) \cdot \left( { - 0,8} \right).\)

c) \(\frac{{ - 3}}{5}:\frac{7}{5} - \frac{3}{5}:\frac{7}{5} + 2\frac{3}{5}.\)       

d) \(\left( {\frac{5}{7} \cdot 0,6 - 5:3\frac{1}{2}} \right) \cdot \left( {40\%  - 1,4} \right) \cdot {\left( { - \frac{2}{3}} \right)^3}.\)

Hai bạn Dũng và Nam chơi 1 ván oẳn tù tì gồm 10 lần theo luật chơi: Búa (B) thắng Kéo (K); Kéo (K) thắng Lá (L), Lá (L) thắng Búa (B) và hòa nhau nếu cùng loại.

     Sau đây là kết quả của mỗi ván chơi:

         a) Hãy bổ sung kết quả ván chơi để hoàn thành bảng thống kê trên.

         b) Tính xác suất thực nghiệm của sự kiện “Dũng không thua Nam”.

Một cửa hàng nhập về 100 cái áo với giá gốc mỗi cái là 250 000 đồng. Cửa hàng đã bán 60 cái áo với giá mỗi cái lãi \(25\% \) so với giá gốc; 40 cái áo còn lại bán lỗ \(5\% \) so với giá gốc. Hỏi sau khi bán hết 100 cái áo cửa hàng đó lãi hay lỗ bao nhiêu tiền?

     1) Cho điểm \(O\) thuộc đường thẳng \(xy.\) Trên tia \(Oy\) lấy điểm \(A\) và \(B\) sao cho \(OA = 3{\rm{\;cm}}\) và \(OB = 5{\rm{\;cm}}.\)

a) Trong ba điểm \(O,\,\,A,\,\,B\) thì điểm nào nằm giữa?

b) Tính độ dài đoạn thẳng \(AB.\)

c) Lấy điểm \(C\) thuộc tia \(Ox\) sao cho \(AC = 6{\rm{\;cm}}.\) Điểm \(O\) có phải là trung điểm của đoạn thẳng \(AC\) không? Tại sao?

2) Cho hình vẽ bên, biết \[\widehat {xOy} = 20^\circ ,\] \[\widehat {yOz} = 15^\circ ,\] \[\widehat {zOt} = 30^\circ ,\] \[\widehat {tOu} = 25^\circ .\]

        a) Sắp xếp các góc: \[\widehat {xOy},\] \[\widehat {yOz},\] \[\widehat {zOt},\] \[\widehat {tOu}\] theo thứ tự số đo tăng dần và cho biết các góc này là loại góc gì (góc bẹt, góc vuông, góc nhọn, góc tù)?

        b) Biết rằng \(\widehat {xOu} = \widehat {xOy} + \widehat {yOz} + \widehat {zOt} + \widehat {tOu}.\) Hãy cho biết góc \(xOu\) là loại góc gì.