2.1. Tính giá trị của biểu thức \(A = \frac{{x + {y^2}}}{5} + xy\) tại \(x = 1,y = 3\).
2.2. Cho hai đa thức: \(A\left( x \right) = 2{x^4} + 3{x^2} - x + 3 - {x^2} - {x^4} - 6{x^3}\);
\(B\left( x \right) = 10{x^3} + 3 - {x^4} - 4{x^3} + 4x - 2{x^2}\).
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến.
b) Xác định bậc và hệ số cao nhất của đa thức \(A\left( x \right)\).
c) So sánh \(A\left( { - 1} \right)\) và \(B\left( 1 \right)\).
d) Tìm đa thức \(M\left( x \right)\) sao cho \(A\left( x \right) = M\left( x \right) - B\left( x \right)\). Tìm nghiệm của đa thức \(M\left( x \right)\).
2.1. Tính giá trị của biểu thức \(A = \frac{{x + {y^2}}}{5} + xy\) tại \(x = 1,y = 3\).
2.2. Cho hai đa thức: \(A\left( x \right) = 2{x^4} + 3{x^2} - x + 3 - {x^2} - {x^4} - 6{x^3}\);
\(B\left( x \right) = 10{x^3} + 3 - {x^4} - 4{x^3} + 4x - 2{x^2}\).
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến.
b) Xác định bậc và hệ số cao nhất của đa thức \(A\left( x \right)\).
c) So sánh \(A\left( { - 1} \right)\) và \(B\left( 1 \right)\).
d) Tìm đa thức \(M\left( x \right)\) sao cho \(A\left( x \right) = M\left( x \right) - B\left( x \right)\). Tìm nghiệm của đa thức \(M\left( x \right)\).
Quảng cáo
Trả lời:
2.1. Thay \(x = 1,y = 3\) vào biểu thức \(A = \frac{{x + {y^2}}}{5} + xy\), ta được: \(A = \frac{{1 + {3^2}}}{5} + 1.3 = 5\).
Vậy giá trị của biểu thức \(A = 5\) khi \(x = 1,y = 3\).
2.2. a) \(A\left( x \right) = 2{x^4} + 3{x^2} - x + 3 - {x^2} - {x^4} - 6{x^3}\)
\( = \left( {2{x^4} - {x^4}} \right) - 6{x^3} + \left( {3{x^2} - {x^2}} \right) - x + 3\)
\( = {x^4} - 6{x^3} + 2{x^2} - x + 3\).
\(B\left( x \right) = 10{x^3} + 3 - {x^4} - 4{x^3} + 4x - 2{x^2}\)
\( = - {x^4} + \left( {10{x^3} - 4{x^3}} \right) - 2{x^2} + 4x + 3\)
\( = - {x^4} + 6{x^3} - 2{x^2} + 4x + 3\).
b) Đa thức \(A\left( x \right)\) có bậc là 4, hệ số cao nhất là \(1\).
c) Ta có \(A\left( { - 1} \right) = {\left( { - 1} \right)^4} - 6.{\left( { - 1} \right)^3} + 2.{\left( { - 1} \right)^2} - \left( { - 1} \right) + 3\)
\( = 1 + 6 + 2 + 1 + 3 = 13\)
\(B\left( 1 \right) = - {1^4} + {6.1^3} - {2.1^2} + 4.1 + 3\)
\( = - 1 + 6 - 2 + 4 + 3 = 10\)
Do \(13 > 10\) nên \(A\left( { - 1} \right) > B\left( 1 \right)\).
d) Ta có \(A\left( x \right) = M\left( x \right) - B\left( x \right)\)
Suy ra \(M\left( x \right) = A\left( x \right) + B\left( x \right)\)
\(M\left( x \right) = \left( {{x^4} - 6{x^3} + 2{x^2} - x + 3} \right) + \left( { - {x^4} + 6{x^3} - 2{x^2} + 4x + 3} \right)\)
\[ = {x^4} - 6{x^3} + 2{x^2} - x + 3 - {x^4} + 6{x^3} - 2{x^2} + 4x + 3\]
\[ = \left( {{x^4} - {x^4}} \right) + \left( { - 6{x^3} + 6{x^3}} \right) + \left( {2{x^2} - 2{x^2}} \right) + \left( { - x + 4x} \right) + \left( {3 + 3} \right)\]
\[ = 3x + 6.\]
Để tìm nghiệm của đa thức \(M\left( x \right)\), ta cho \(M\left( x \right) = 0\)
Do đó \(3x + 6 = 0\), suy ra \(x = - 2\).
Vậ y \(x = - 2\) là nghiệm của đa thức \(M\left( x \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì xác suất thực nghiệm xuất hiện mặt sấp là \(\frac{4}{9} = \frac{{4k}}{{9k}}\) \(\left( {k \in {\mathbb{N}^*}} \right)\).
Do đó, tổng số lần tung đồng xu là \(9.k\) (lần).
Số lần xuất hiện mặt sấp là \(4.k\) (lần)
Suy ra số lần xuất hiện mặt ngửa là \(9.k - 4.k = 5.k\) (lần).
Mà tích số lần xuất hiện mặt ngửa và mặt sấp là \(500\) nên ta có: \(4k.5k = 500\) hay \(20.{k^2} = 500\).
Suy ra \({k^2} = 25\) và \(k = 5\)\(\left( {k \in {\mathbb{N}^*}} \right)\).
Do đó, bạn Hanh đã tung đồng xu số lần là: \(9.5 = 45\) (lần).
Lời giải
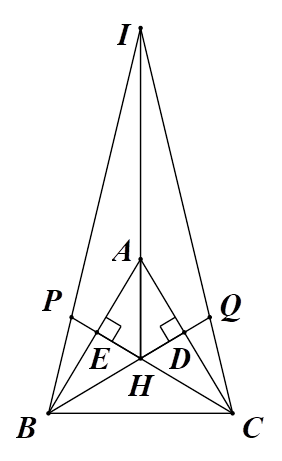
a) Xét \(\Delta ABD\) và \(\Delta ACE\), có:
\(\widehat {ADB} = \widehat {AEC} = 90^\circ \);
\[AB = AC\] (do \(\Delta ABC\) cân tại \(A\));
\(\widehat {BAC}\) là góc chung.
Do đó \(\Delta ABD = \Delta ACE\) (cạnh huyền – góc nhọn).
Suy ra \(\widehat {ABD} = \widehat {ACE}\) (cặp góc tương ứng).
b) Ta có \(\widehat {ABD} = \widehat {ACE}\) (câu a)
Lại có \(\widehat {ABC} = \widehat {ACB}\) (do \(\Delta ABC\) cân tại \(A\)).
Do đó \(\widehat {ABC} - \widehat {ABD} = \widehat {ACB} - \widehat {ACE}\) hay \(\widehat {HBC} = \widehat {HCB}\).
\(\Delta BHC\) có \(\widehat {HBC} = \widehat {HCB}\) nên là tam giác cân tại \(H\).
Suy ra \(HB = HC\,\,\,\,\left( 1 \right)\)
Ta có \(\Delta HCD\) vuông tại \(D\) nên cạnh huyền \(HC\) là lớn nhất.
Do đó \(HC > HD\,\,\,\,\left( 2 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có \(HB > HD\).
c) Gọi \(I\) là giao điểm của \(BP\) và \(CQ\).
Xét \(\Delta BPH\) và \(\Delta CQH\), có:
\(HP = HQ\) (giả thiết);
\(\widehat {BHP} = \widehat {CHQ}\) (hai góc đối đỉnh);
\(HB = HC\) (câu b).
Do đó \(\Delta BPH = \Delta CQH\,\,\left( {{\rm{c}}{\rm{.g}}{\rm{.c}}} \right)\).
Suy ra \(\widehat {HBP} = \widehat {HCQ}\) (cặp góc tương ứng).
Mà \(\widehat {HBC} = \widehat {HCB}\) (câu b).
Suy ra \(\widehat {HBC} + \widehat {HBP} = \widehat {HCB} + \widehat {HCQ}\) hay \(\widehat {IBC} = \widehat {ICB}\).
\(\Delta IBC\) có \(\widehat {IBC} = \widehat {ICB}\) nên là tam giác cân tại \(I\).
Suy ra \(IB = IC\).
Mà \(AB = AC\) (câu a) và \(HB = HC\) (câu b).
Do đó ba điểm \(I\), \(A\), \(H\) cùng nằm trên đường trung trực của đoạn thẳng \(BC\).
Hay \(I\), \(A\), \(H\) thẳng hàng.
Vậy ba đường thẳng \(BP\), \(CQ\), \(AH\) đồng quy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.