Câu hỏi:
30/06/2025 4
1. Bóng của một cái tháp trên mặt đất có độ dài \[BC = 63{\rm{ m}}.\] Cùng thời điểm đó, một cây cột \[DE\] cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m (hình vẽ). Tính chiều cao của tháp.
![1. Bóng của một cái tháp trên mặt đất có độ dài \[BC = 63{\rm{ m}}.\] Cùng thời điểm đó, một cây cột \[DE\] cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m (hình vẽ). Tính chiều cao của tháp. 2. Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\] a) Chứng minh: . b) Chứng minh: \(AE \cdot AC = AF \cdot AB\). c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid4-1751277199.png)
2. Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\]
a) Chứng minh: .
b) Chứng minh: \(AE \cdot AC = AF \cdot AB\).
c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\]
1. Bóng của một cái tháp trên mặt đất có độ dài \[BC = 63{\rm{ m}}.\] Cùng thời điểm đó, một cây cột \[DE\] cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m (hình vẽ). Tính chiều cao của tháp.
2. Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\]
a) Chứng minh: .
b) Chứng minh: \(AE \cdot AC = AF \cdot AB\).
c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Ta có \(AB \bot BC;\,\,DE \bot BC\) nên \(DE\,{\rm{//}}\,AB\).
Xét tam giác \(ABC\) có \(DE\,{\rm{//}}\,AB\), ta có
\[\frac{{DE}}{{AB}} = \frac{{CE}}{{CB}}\] (hệ quả của định lí Thalès).
Hay \[\frac{2}{{AB}} = \frac{3}{{63}}\] suy ra \[AB = 42\,\,{\rm{m}}\].
Vậy chiều cao của tháp là 42 m.
2.
![1. Bóng của một cái tháp trên mặt đất có độ dài \[BC = 63{\rm{ m}}.\] Cùng thời điểm đó, một cây cột \[DE\] cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m (hình vẽ). Tính chiều cao của tháp. 2. Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\] a) Chứng minh: . b) Chứng minh: \(AE \cdot AC = AF \cdot AB\). c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid3-1751277175.png)
a) Xét \[\Delta ABK\] và \[\Delta CBF\] có:
\[\widehat {ABK} = \widehat {CBF}\;\left( {\widehat B\;\,{\rm{chung}}} \right)\]; \(\widehat {AKB} = \widehat {CFB}\;\left( { = 90^\circ } \right)\)
Do đó .
b) Xét \[\Delta AEB\] và \[\Delta ACF\] có:
\(\widehat {EAB} = \widehat {FAC}\;\,\left( {\widehat A\;\,{\rm{chung}}} \right)\); \(\widehat {AEB} = \widehat {AFC}\;\left( { = 90^\circ } \right)\)
Do đó
Suy ra \(\frac{{AE}}{{AF}} = \frac{{AB}}{{AC}}\) hay \(AE \cdot AC = AF \cdot AB\) (đpcm)
c) Xét \[\Delta BFC\] vuông tại \[F\] có \[O\] là trung điểm của \[BC\] nên \(FO = \frac{{BC}}{2}\).
Xét \[\Delta BEC\] vuông tại \[E\] có \[O\] là trung điểm của \[BC\] nên \(EO = \frac{{BC}}{2}\).
Do đó \[FO = EO = \frac{{BC}}{2}\]. (1)
Xét \[\Delta AEH\] vuông tại \[E\] có \[I\] là trung điểm của \[AH\] nên \(EI = \frac{{AH}}{2}\).
Xét \[\Delta AFH\] vuông tại \[F\] có \[I\] là trung điểm của \[AH\] nên \(FI = \frac{{AH}}{2}\).
Do đó \[FI = EI = \frac{{AH}}{2}\]. (2)
Từ (1) và (2) ta suy ra được \[OI\] là đường trung trực của cạnh \[EF\].
Khi đó \[OI \bot EF\] hay \[OI \bot DN\].
Do đó \[DN\] là đường cao của \[\Delta DOI\].
Xét \[\Delta DOI\] có \[DN\] và \[IK\] là đường cao và \[N\] là giao của \[DN\] và \[IK\].
Do đó \[N\] là trực tâm của tam giác \[DOI\].
Vậy \[OI \bot DI\] (đpcm).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \[x\] (viên) số bi đỏ trong túi \[\left( {0 < x < 48} \right).\]
Khi đó, số bi xanh trong túi là \[\left( {48--x} \right)\] viên.
Xác suất lấy được viên bi màu đỏ là \[\frac{x}{{48}}.\]
Xác suất lấy được viên bi màu xanh là: \[\frac{{48 - x}}{{48}}.\]
Theo đề bài, xác suất lấy được viên bi màu đỏ bằng 92% xác suất lấy được viên bi màu xanh nên ta có phương trình \[\frac{x}{{48}} = 92\% \cdot \frac{{48 - x}}{{48}}\]
\[x = 0,92\left( {48 - x} \right)\]
\[x = 44,16 - 0,92x\]
\[1,92x = 44,16\]
\[x = 23\] (TMĐK)
Vậy số viên bi màu đỏ và viên bi màu xanh có trong túi lần lượt là 23 viên và 25 viên.
Lời giải
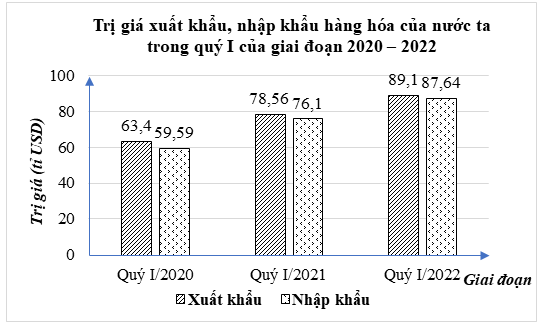
1. a) Từ biểu đồ cột kép, ta hoàn thành được bảng thống kê như sau:
|
Giai đoạn |
Quý I/2020 |
Quý I/2021 |
Quý I/2022 |
|
Xuất khẩu |
\[63,4\] |
\[78,56\] |
\[89,1\] |
|
Nhập khẩu |
\[59,59\] |
\[76,1\] |
\[87,64\] |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2 022 là:
\[63,4 + 78,56 + 89,1 = 231,06\] (tỉ USD)
Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2 022 là:
\[59,59 + 76,1 + 87,64 = 223,33\] (tỉ USD)
c) Ta thấy trị giá xuất khẩu hàng hóa của quý I/2021 lớn hơn trị giá xuất khẩu hàng hóa của quý I/2020 (vì \[78,56 > 63,4\]).
Do đó, giá trị xuất khẩu hàng hóa của nước ta trong quý I năm 2021 tăng so với quý I năm 2020.
Tỉ số phần trăm trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 và quý I năm 2021 là: \(\frac{{78,56}}{{63,4}} \cdot 100\% \approx 123,9\% \).
Số phần trăm giá trị xuất khẩu hàng hóa của nước ta trong quý I năm 2021 tăng so với quý I năm 2020 là khoảng: \[123,9\% - 100\% = 23,9\% \].
Vậy giá trị xuất khẩu hàng hóa của nước ta trong quý I năm 2021 tăng khoảng \[19,3\% \] so với quý I năm 2020.
2. a) Tập hợp \(K\) gồm các kết quả xảy ra đối với thành viên được chọn là :
K = {Kon Tum; Bình Phước; Tây Ninh; Bình Dương; Gia Lai; Bà Rịa – Vũng Tàu; Đồng Nai; Đăk Lăk; Đăk Nông; Lâm Đồng; Thành phố Hồ Chí Minh}.
Số phần tử của tập hợp \(K\) là 11.
b) Có 5 kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Tây Nguyên” đó là Kon Tum; Gia Lai; Đăk Lăk; Đăk Nông; Lâm Đồng.
Vì thế xác suất của biến cố đó là \(\frac{5}{{11}}\).
c) Có 6 kết quả thuận lợi cho biến cố “Thành viên được chọn ra đến từ vùng Đông Nam Bộ” đó là Bình Phước; Tây Ninh; Bình Dương; Bà Rịa – Vũng Tàu; Đồng Nai; Thành phố Hồ Chí Minh.
Vì thế xác suất của biến cố đó là \(\frac{6}{{11}}\).
Câu 3
a) \[7x - \left( {12 + 5x} \right) = 6\];
b) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\).
2. Giải bài toán sau bằng cách lập phương trình bậc nhất một ẩn:
Anh Long muốn mua một điện thoại di động iPhone 16 Pro để tặng vợ. Cửa hàng di động có chương trình khuyến mãi lớn, giảm 10% so với giá ban đầu. Do anh Long là khách hàng VIP nên được giảm thêm 5% so với giá đã giảm. Tổng số tiền giảm hai lần là \[3\,\,915\,\,000\] đồng. Hỏi giá ban đầu của điện thoại iPhone 16 Pro là bao nhiêu?
a) \[7x - \left( {12 + 5x} \right) = 6\];
b) \(\frac{{8x - 3}}{4} - \frac{{3x - 2}}{2} = \frac{{2x - 1}}{2} + \frac{{x + 3}}{4}\).
2. Giải bài toán sau bằng cách lập phương trình bậc nhất một ẩn:
Anh Long muốn mua một điện thoại di động iPhone 16 Pro để tặng vợ. Cửa hàng di động có chương trình khuyến mãi lớn, giảm 10% so với giá ban đầu. Do anh Long là khách hàng VIP nên được giảm thêm 5% so với giá đã giảm. Tổng số tiền giảm hai lần là \[3\,\,915\,\,000\] đồng. Hỏi giá ban đầu của điện thoại iPhone 16 Pro là bao nhiêu?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo