Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao hàng tháng. Một phần đường thẳng \(d\) ở hình dưới đây biểu thị chi phí (đơn vị: triệu đồng) để sử dụng dịch vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng).
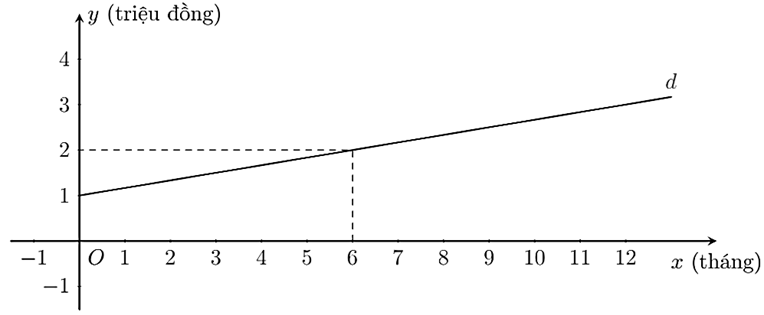
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng \(d.\)
b) Giao điểm của đường thẳng \(d\) với trục tung trong tình huống này có ý nghĩa gì? Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng.
Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao hàng tháng. Một phần đường thẳng \(d\) ở hình dưới đây biểu thị chi phí (đơn vị: triệu đồng) để sử dụng dịch vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng).
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng \(d.\)
b) Giao điểm của đường thẳng \(d\) với trục tung trong tình huống này có ý nghĩa gì? Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Gọi hàm số bậc nhất cần tìm là \(y = ax + b\,\,\left( {a \ne 0} \right).\)
Theo giả thiết, ta có
• Với \(x = 0\,;\,\,y = 1\) thì \(0a + b = 1\) hay \(b = 1\).
• Với \(x = 6\,;\,\,y = 2\) thì \(6a + 1 = 2\) hay \(a = \frac{1}{6}\).
Vậy \(\left( d \right):y = \frac{1}{6}x + 1\).
b) Giao điểm của đường thẳng \(d\) với trục tung có ý nghĩa là chi phí ban đầu người dùng trả cho nhà mạng là 1 triệu đồng.
Trong thời gian 12 tháng, người dùng phải trả số tiền là: \(\frac{1}{6} \cdot 12 + 1 = 3\) (triệu đồng).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Tổng khối lượng các loại hạt điều thu hoạch được là:
\(1\,\,450 + 2\,\,230 + 1\,\,860 = 5\,\,540\) (kg).
Vậy tổng khối lượng các loại hạt điều thu hoạch được là \(5\,\,540\) kg.
b) Tổng khối lượng hạt điều loại 2 và loại 3 là: \(2\,\,230 + 1\,\,860 = 4\,\,090\) (kg).
Xác suất thực nghiệm của biến cố B là \(P\left( B \right) = \frac{{4\,\,090}}{{5\,\,540}} \approx 0,7383.\)
c) Gọi \(k\) là số kilôgam hạt điều loại 1 trong \(100\) kg hạt điều sau khi phân loại.
Ta có \[P\left( A \right) = \frac{k}{{100}} \approx 0,2617\] suy ra \(k \approx 0,2617 \cdot 100 = 26,17 \approx 26\) (kg).
Vậy có khoảng 26 kg hạt điều loại 1 trong 100 kg hạt điều sau khi phân loại.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Tổng số sản phẩm loại A và loại B là \(10 + 7 = 17\) (sản phẩm).
Khi lấy ngẫu nhiên 2 sản phẩm:
Chọn sản phẩm thứ nhất chọn 1 trong 17 sản phẩm nên có 17 cách;
Chiếc sản phẩm thứ hai chọn \[1\] trong 16 sản phẩm còn lại nên có 16 cách.
Số cách chọn 2 sản phẩm trong số 17 sản phẩm là: \(\frac{{17.16}}{2} = 136\) (cách) (cứ mỗi cặp bị lặp lại 2 lần).
Có \(\frac{{10.9}}{2} = 45\) cách chọn chỉ lấy ra 2 sản phẩm loại A.
Số kết quả thuận lợi của biến cố E là \[136--45 = 91.\]
Vậy xác suất của biến cố E là \(\frac{{91}}{{136}}\).
![1. Người ta dùng máy ảnh để chụp một người có chiều cao \[1,5{\rm{ m}}\] (như hình vẽ). Sau khi rửa phim thấy ảnh \[CD\] cao \[4{\rm{ cm}}\]. Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là \[ED = 6{\rm{ cm}}.\] Hỏi khoảng cách từ người đó đến vật kính máy ảnh một đoạn \[BE\] là bao nhiêu? 2. Cho tam giác \[ABC\] vuông tại \[A\,\,\,\left( {AB < AC} \right),\] vẽ đường cao \[AH.\] a) Chứng minh: . b) Chứng minh: \(A{H^2} = HB \cdot HC\). c) Trên tia \[HC,\] lấy điểm \(D\) sao cho \[HD = HA.\] Từ \(D\) vẽ đường thẳng song song \[AH\] cắt \[AC\] tại \[E.\] Chứng minh \[AE = AB.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid6-1751333903.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập