3.1. Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right),\) biết \(\widehat {ABC} = 106^\circ .\)
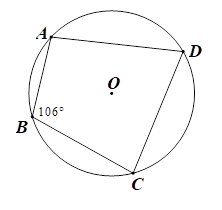
Tính số đo cung \(ADC\).
3.2. Cho hình lục giác đều \(ABCDEG\) (các đỉnh của lục giác theo thứ tự cùng chiều kim đồng hồ) có tâm \(O.\) Phép quay ngược chiều tâm \(O\) biến điểm \(A\) thành điểm \(E\) có góc quay là bao nhiêu độ?
3.1. Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right),\) biết \(\widehat {ABC} = 106^\circ .\)

Tính số đo cung \(ADC\).
3.2. Cho hình lục giác đều \(ABCDEG\) (các đỉnh của lục giác theo thứ tự cùng chiều kim đồng hồ) có tâm \(O.\) Phép quay ngược chiều tâm \(O\) biến điểm \(A\) thành điểm \(E\) có góc quay là bao nhiêu độ?
Quảng cáo
Trả lời:
3.1. Vì tứ giác \(ABCD\) nội tiếp nên \(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (tổng hai góc đối của tứ giác nội tiếp)
Suy ra \(\widehat {ADC} = 180^\circ - \widehat {ABC} = 180^\circ - 106^\circ = 74^\circ .\)
Khi đó, (số đo cung gấp hai lần số đo góc nội tiếp chắn cung đó).
3.2.
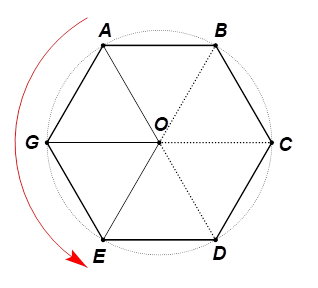
Vì \(ABCDEG\) là lục giác đều nên \(AB = BC = CD = DE = EG = GA\) và Xét \(\Delta OAB\) và \(\Delta OBC\) có:
\(OA = OB,\,\,OB = OC,\,\,AB = BC\)
Do đó \(\Delta OAB = \Delta OBC\) (c.c.c)
Suy ra \(\widehat {AOB} = \widehat {BOC}\) (hai góc tương ứng).
Tương tự, ta sẽ chứng minh được
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOG} = \widehat {GOA}.\)
Lại có \(\widehat {AOB} + \widehat {BOC} + \widehat {COD} + \widehat {DOE} + \widehat {EOG} + \widehat {GOA} = 360^\circ \).
Suy ra \(6\widehat {GOA} = 360^\circ \) nên \[\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOG} = \widehat {GOA} = 60^\circ .\]
Do đó, \(\widehat {AOE} = \widehat {GOA} + \widehat {EOG} = 60^\circ + 60^\circ = 120^\circ .\)
Lại có \(OA = OE.\) Như vậy, phép quay ngược chiều \(120^\circ \) tâm \(O\) biến điểm \(A\) thành điểm \(E.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đối tượng thống kê là chiều cao của 50 cây giống sau 20 ngàu gieo hạt.
Tiêu chí thống kê là tỉ lệ phần trăm tương ứng theo từng nhóm.
b) Các cây giống có chiều cao dưới \(13{\rm{ cm}}\) chiếm số phần trăm là: \(16 + 24 = 40\% \).
c) Ta có biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng của mẫu dữ liệu mà Huy thu thập được là:
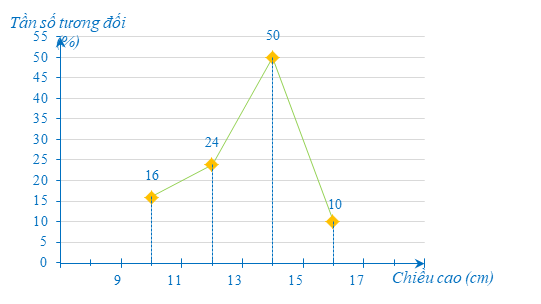
d) Ta tính tần số của các nhóm số liệu như sau:
⦁ Tần số của nhóm \(\left[ {9;\,\,11} \right)\) là: \(\frac{{16 \cdot 50}}{{100}} = 8.\)
⦁ Tần số của nhóm \(\left[ {11;\,\,13} \right)\) là: \(\frac{{24 \cdot 50}}{{100}} = 12.\)
⦁ Tần số của nhóm \(\left[ {13;\,\,15} \right)\) là: \(\frac{{50 \cdot 50}}{{100}} = 25.\)
⦁ Tần số của nhóm \(\left[ {15;\,\,17} \right)\) là: \(\frac{{10 \cdot 50}}{{100}} = 5.\)
Bảng tần số ghép nhóm cho mẫu dữ liệu Huy thu thập được như sau:
|
Chiều cao (cm) |
\(\left[ {9;\,\,11} \right)\) |
\(\left[ {11;\,\,13} \right)\) |
\(\left[ {13;\,\,15} \right)\) |
\(\left[ {15;\,\,17} \right)\) |
|
Tần số |
8 |
12 |
25 |
5 |
Lời giải
|
a) Xét đường tròn \(\left( O \right)\) có \(AC\) là đường kính nên \(\widehat {ABC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn). Xét đường tròn \(\left( {O'} \right)\) có \(AF\) là đường kính nên \(\widehat {ABF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn). Do đó \(\widehat {CBF} = \widehat {ABC} + \widehat {ABF} = 90^\circ + 90^\circ = 180^\circ .\) Suy ra ba điểm \(C,\,\,B,\,\,F\) thẳng hàng. Chứng minh tương tự như trên, ta có \(\widehat {ADC} = 90^\circ \) |
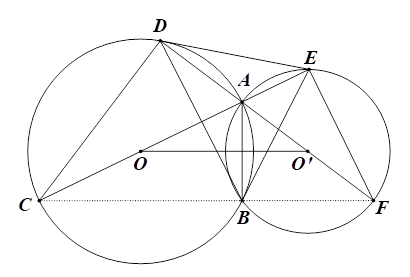 |
(góc nội tiếp chắn nửa đường tròn \(\left( O \right))\) và \(\widehat {AEF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn \(\left( {O'} \right)).\)
Do đó \(\widehat {CDF} = \widehat {CEF} = 90^\circ \) nên đường tròn ngoại tiếp các tam giác vuông \(CDF,\,\,CEF\) có tâm là trung điểm của cạnh huyền \(CF\) hay các điểm \(C,\,\,D,\,\,E,\,\,F\) cùng nằm trên đường tròn đường kính \(CF.\)
Vậy tứ giác \(CDEF\) nội tiếp đường tròn đường kính \(CF.\)
b) Tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) nên \(\widehat {ABD} = \widehat {ACD}\) (hai góc nội tiếp cùng chắn cung \(AD)\)
Tứ giác \(ABFE\) nội tiếp đường tròn \(\left( {O'} \right)\) nên \(\widehat {ABE} = \widehat {AFE}\) (hai góc nội tiếp cùng chắn cung \(AE)\)
Tứ giác \(CDEF\) nội tiếp đường tròn đường kính \(CF\) nên \(\widehat {DCE} = \widehat {DFE}\) (hai góc nội tiếp cùng chắn cung \(DE)\) hay \(\widehat {ACD} = \widehat {AFE}\).
Từ đó suy ra \(\widehat {ABD} = \widehat {ABE}\) hay \(BA\) là tia phân giác của góc \(DBE.\)
Chứng minh tương tự, ta có \(\widehat {CED} = \widehat {BEC}\left( { = \widehat {CFD}} \right)\) hay \(EC\) là tia phân giác của góc \(BED.\)
Xét tam giác \(BDE\) có \(BA\) và \(EC\) là hai đường phân giác của tam giác, chúng cắt nhau tại \(A\) nên \(A\) là tâm đường tròn nội tiếp tam giác \(BDE.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.