(0,5 điểm) Cho hai số thực \[a,\,\,b\] thỏa mãn \[a + b \ne 0.\] Chứng minh bất đẳng thức sau:
\({a^2} + {b^2} + {\left( {\frac{{ab + 1}}{{a + b}}} \right)^2} \ge 2.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Với hai số thực \[a,\,\,b\] thỏa mãn \[a + b \ne 0\], ta có:
\({a^2} + {b^2} + {\left( {\frac{{ab + 1}}{{a + b}}} \right)^2} - 2 = {a^2} + {b^2} + \frac{{{{\left( {ab + 1} \right)}^2}}}{{{{\left( {a + b} \right)}^2}}} - 2\)
\( = {a^2} + {b^2} + 2ab - 2ab + \frac{{{{\left( {ab + 1} \right)}^2}}}{{{{\left( {a + b} \right)}^2}}} - 2\)
\( = {\left( {a + b} \right)^2} - 2ab + \frac{{{{\left( {ab + 1} \right)}^2}}}{{{{\left( {a + b} \right)}^2}}} - 2\)
\( = {\left( {a + b} \right)^2} - 2\left( {ab + 1} \right) + \frac{{{{\left( {ab + 1} \right)}^2}}}{{{{\left( {a + b} \right)}^2}}}\)
\[ = \frac{{{{\left( {a + b} \right)}^4} - 2{{\left( {a + b} \right)}^2}\left( {ab + 1} \right) + {{\left( {ab + 1} \right)}^2}}}{{{{\left( {a + b} \right)}^2}}}\]
\[ = \frac{{{{\left[ {{{\left( {a + b} \right)}^2} - \left( {ab + 1} \right)} \right]}^2}}}{{{{\left( {a + b} \right)}^2}}}\].
Với \[a + b \ne 0\] ta có \({\left( {a + b} \right)^2} > 0\) và \[{\left[ {{{\left( {a + b} \right)}^2} - \left( {ab + 1} \right)} \right]^2} \ge 0\]
Do đó \[\frac{{{{\left[ {{{\left( {a + b} \right)}^2} - \left( {ab + 1} \right)} \right]}^2}}}{{{{\left( {a + b} \right)}^2}}} \ge 0\] nên \({a^2} + {b^2} + {\left( {\frac{{ab + 1}}{{a + b}}} \right)^2} - 2 \ge 0\) hay \({a^2} + {b^2} + {\left( {\frac{{ab + 1}}{{a + b}}} \right)^2} \ge 2.\)
Vậy bất đẳng thức \({a^2} + {b^2} + {\left( {\frac{{ab + 1}}{{a + b}}} \right)^2} \ge 2\) đã được chứng minh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\sin C = 2,6\).
B. \(\sin C \approx 0,385\).
C. \(\sin C \approx 0,4\).
D. \(\sin C \approx 0,38\).
Lời giải
Đáp án đúng là: D
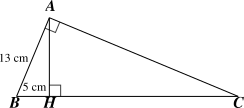
Xét \(\Delta ABC\) vuông tại \(A\), ta có \(\widehat {B\,} + \widehat {C\,} = 90^\circ \) hay hai góc \(B\) và \(C\) phụ nhau, do đó \(\sin C = \cos B\).
Xét \(\Delta ABH\) vuông tại \(H\), ta có:
\(\cos B = \frac{{BH}}{{AB}} = \frac{5}{{13}} \approx 0,38\).
Vậy \(\sin C = \cos B \approx 0,38\).
Câu 2
(2,0 điểm)
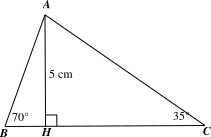
1. Cho tam giác \(ABC\) có đường cao \(AH = 5\,\,{\rm{cm}},\,\,\widehat {B\,} = 70^\circ ,\,\,\widehat {C\,} = 35^\circ .\) Tính độ dài các cạnh của tam giác \(ABC\) (làm tròn kết quả đến chữ số thập phân thứ hai).
|
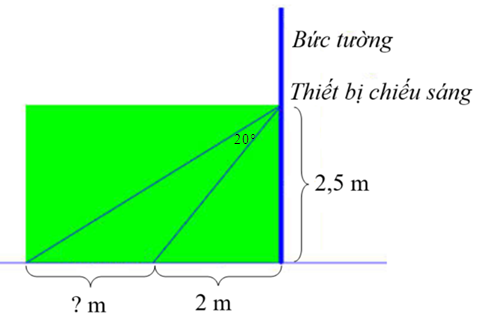
2. Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm như hình vẽ. Thiết bị này có góc chiếu sáng là \(20^\circ \) và cần đặt cao hơn mặt đất là \(2,5\,\,{\rm{m}}.\) Người ta đặt thiết bị chiếu sáng này sát tường và được canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường \(2\,\,{\rm{m}}.\) Tính độ dài vùng được chiếu sáng trên mặt đất (làm tròn kết quả đến chữ số thập phân thứ nhất). |
|
Lời giải
Hướng dẫn giải
|
1. Xét tam giác \(AHB\) vuông tại \(H\) ta có: ⦁ \(\sin B = \frac{{AH}}{{AB}}\), suy ra \(AB = \frac{{AH}}{{\sin B}} = \frac{5}{{\sin 70^\circ }} \approx 5,32{\rm{\;(cm);}}\) ⦁ \[BH = AH \cdot \cot B = 5 \cdot \cot 70^\circ \approx 1,82{\rm{\;(cm)}}{\rm{.}}\] Xét tam giác \(AHC\) vuông tại \(H\) ta có: ⦁ \(\sin C = \frac{{AH}}{{AC}}\), suy ra \(AC = \frac{{AH}}{{\sin C}} = \frac{5}{{\sin 35^\circ }} \approx 8,72{\rm{\;(cm);}}\) ⦁ \(CH = AH \cdot \cot C = 5 \cdot \cot 35^\circ \approx 7,14{\rm{\;(cm)}}{\rm{.}}\) Khi đó \(BC = BH + HC \approx 1,82 + 7,14 = 8,96{\rm{\;(cm)}}{\rm{.}}\) Vậy \(AB \approx 5,32\,\,{\rm{cm}}\,{\rm{,}}\,\,AC \approx 8,72\,\,{\rm{cm}}\,{\rm{,}}\,\,BC \approx 8,96\,\,{\rm{cm}}\,.\) |
|
2. Hình ảnh thiết bị chiếu sáng trong bài toán được mô tả như hình vẽ bên, trong đó \(A\) là vị trí đặt thiết bị chiếu sáng, \(CD\) là độ dài vùng được chiếu sáng trên mặt đất và \(\widehat {CAD} = 20^\circ \) là góc chiếu sáng. Khi đó ta có \(AB = 2,5{\rm{\;m}}\) và \(BC = 2{\rm{\;m}}.\)
⦁ Xét \(\Delta ABC\) vuông tại \(B\), ta có:
\(\tan \widehat {BAC} = \frac{{BC}}{{AB}} = \frac{2}{{2,5}} = 0,8\) nên \(\widehat {BAC} \approx 38,7^\circ .\)
Ta có \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD} \approx 38,7^\circ + 20^\circ = 58,7^\circ .\)
⦁ Xét \(\Delta ABD\) vuông tại \(B\), ta có
\(BD = AB \cdot \tan \widehat {BAD} \approx 2,5 \cdot \tan 58,7^\circ \approx 4,1{\rm{\;(m)}}{\rm{.}}\)
Do đó \(CD = BD - BC \approx 4,1 - 2 = 2,1{\rm{\;(m)}}{\rm{.}}\)
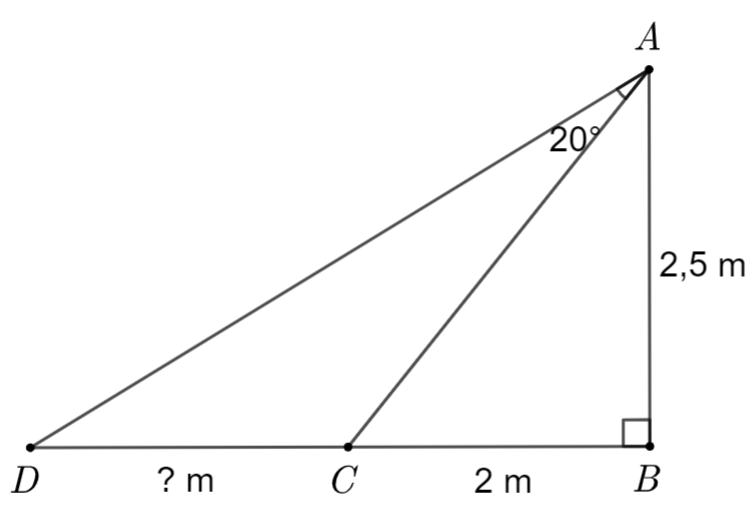
Vậy độ dài vùng được chiếu sáng trên mặt đất khoảng \(2,1\) mét.
Câu 3
A. \(x > - 10\).
B. \[x \ge - 10\].
C. \(x < - 10\).
</>
D. \(x \le - 10\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 0.
B. 1.
C. 2.
D. Vô số.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.