Câu hỏi:
05/07/2025 31(2,5 điểm) Giải phương trình và bất phương trình sau:
1. Giải các phương trình sau:
a) \[4x\left( {x - 3} \right) - 3x + 9 = 0\];
b) \(\frac{{12}}{{1 - 9{x^2}}} = \frac{{1 - 3x}}{{1 + 3x}} - \frac{{1 + 3x}}{{1 - 3x}};\)
2. Giải các bất phương trình sau:
a) \(3x - 8 > 4x - 12;\)
b) \[\frac{{2x - 1}}{3} - \frac{{x + 2}}{2} < \frac{{5x + 4}}{6};\]
e) \(2x - \frac{{x - 7}}{3} < 9.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
|
1. a) \[4x\left( {x - 3} \right) - 3x + 9 = 0\] \(4x\left( {x - 3} \right) - 3\left( {x - 3} \right) = 0\) \(\left( {4x - 3} \right)\left( {x - 3} \right) = 0\) \(4x - 3 = 0\) hoặc \(x - 3 = 0\) \(x = \frac{3}{4}\) hoặc \(x = 3\). Vậy nghiệm của phương trình là \(x = \frac{3}{4}\) và \(x = 3\). |
1. b) \(\frac{{12}}{{1 - 9{x^2}}} = \frac{{1 - 3x}}{{1 + 3x}} - \frac{{1 + 3x}}{{1 - 3x}}\) Điều kiện xác định \(3x + 1 \ne 0\); \(3x - 1 \ne 0\) và \(1 - 9{x^2} \ne 0\) hay \(x \ne - \frac{1}{3}\) và \(x \ne \frac{1}{3}\). Quy đồng mẫu hai vế của phương trình, ta được \(\frac{{12}}{{\left( {1 - 3x} \right)\left( {1 + 3x} \right)}} = \frac{{{{\left( {1 - 3x} \right)}^2}}}{{\left( {1 - 3x} \right)\left( {1 + 3x} \right)}} - \frac{{{{\left( {1 + 3x} \right)}^2}}}{{\left( {1 - 3x} \right)\left( {1 + 3x} \right)}}\) Suy ra \(12 = {\left( {1 - 3x} \right)^2} - {\left( {1 + 3x} \right)^2}\) \(12 = \left( {1 - 3x + 1 + 3x} \right)\left( {1 - 3x - 1 - 3x} \right)\) \[12 = 2\left( { - 6x} \right)\] \[12 = - 12x\] \[x = - 1\]. Giá trị \[x = - 1\] thỏa mãn ĐKXĐ. Vậy nghiệm của phương trình là \[x = - 1\]. |
|
c) \(3x - 8 > 4x - 12\) \(3x - 4x > - 12 + 8\) \( - x > - 4\) \(x < 4\). Vậy nghiệm của bất phương trình đã cho là \(x < 4.\) |
d) \[\frac{{2x - 1}}{3} - \frac{{x + 2}}{2} < \frac{{5x + 4}}{6}.\] \[\frac{{2\left( {2x - 1} \right)}}{6} - \frac{{3\left( {x + 2} \right)}}{6} < \frac{{5x + 4}}{6}\] \[2\left( {2x - 1} \right) - 3\left( {x + 2} \right) < 5x + 4\] \[4x - 2 - 3x - 6 < 5x + 4\] \[x - 8 < 5x + 4\] \[ - 4x < 12\] \[x > - 3\]. Vậy nghiệm của bất phương trình đã cho là \[x > - 3.\] |
|
e) \(2x - \frac{{x - 7}}{3} < 9\) \(6x - \left( {x - 7} \right) < 27\) \(6x - x + 7 < 27\) \(5x + 7 < 27\) \(5x < 27 - 7\) \(5x < 20\) \(x < 4.\) Vậy nghiệm của bất phương trình đã cho là \(x < 4.\) |
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
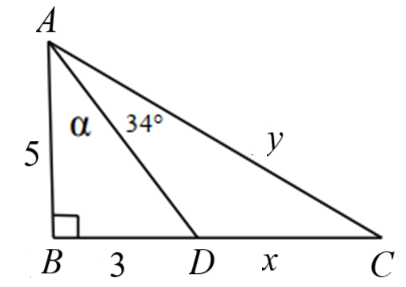
1. Xét \(\Delta ABD\) vuông tại \(A\), ta có: \(\tan \widehat {BAD} = \frac{3}{5}\) suy ra \(\widehat {BAD} \approx 31^\circ \) hay \(\alpha \approx 31^\circ \).
Xét tam giác \(ABC\), ta có: \(\widehat {BAC} = \widehat {BAD} + \widehat {DAC} \approx 31^\circ + 40^\circ = 71^\circ \).
Ta có: \(\tan \widehat {BAC} = \frac{{BC}}{{AB}}\) hay \(BC = AB.\tan \widehat {BAC} \approx 5.\tan 71^\circ \approx 14,52.\)
Lại có \(BD + DC = BC\) hay \(DC \approx 14,52 - 3 = 11,52\) suy ra \(x \approx 11,52.\)
Áp dụng định lý Pythagore vào tam giác \(ABC\), ta có: \(A{B^2} + A{C^2} = B{C^2}\)
Suy ra \(B{C^2} = {5^2} + 14,{5^2} = 235,25\) nên \(BC \approx 15,33\) hay \(y \approx 15,33.\)
Vậy \(\alpha \approx 31^\circ \), \(x \approx 11,52\), \(y \approx 15,33.\)
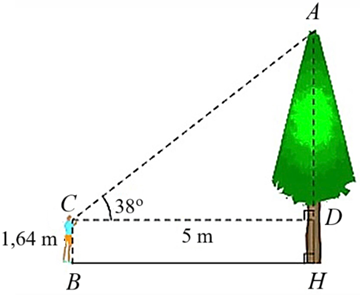
2. Xét tam giác \(ACD\) vuông tại \(D\), ta có: \(AD = CD.\tan \widehat {ACD} = 5.\cos 38^\circ .\)
Ta có chiều cao của cây là \(AH\).
\(AH = AD + DH = 5.\tan 38^\circ + 1,64 \approx 5,55\,\,\left( {\rm{m}} \right){\rm{.}}\)
Vậy chiều cao của cây khoảng \(5,55{\rm{ m}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo