Câu hỏi:
05/07/2025 25(1,0 điểm) Rút gọn các biểu thức sau:
a) \(B = \cot 20^\circ \cdot \cot 40^\circ \cdot \cot 50^\circ \cdot \cot 70^\circ .\)
b) \(A = \cos 40^\circ - \sin 50^\circ + \tan 20^\circ \cot 20^\circ .\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) \(B = \cot 20^\circ \cdot \cot 40^\circ \cdot \cot 50^\circ \cdot \cot 70^\circ \)
\( = \cot 20^\circ \cdot \cot 40^\circ \cdot \tan \left( {90^\circ - 50^\circ } \right) \cdot \tan \left( {90^\circ - 70^\circ } \right)\)
\( = \cot 20^\circ \cdot \cot 40^\circ \cdot \tan 40^\circ \cdot \tan 20^\circ \)
\( = \left( {\cot 20^\circ \cdot \tan 20^\circ } \right) \cdot \left( {\cot 40^\circ \cdot \tan 40^\circ } \right)\)
\( = 1 \cdot 1 = 1.\)
Vậy \(B = 1.\)
b) \(A = \cos 40^\circ - \sin 50^\circ + \tan 20^\circ \cot 20^\circ \)
\( = \cos 40^\circ - \cos 40^\circ + 1\)
\( = 0 + 1 = 1.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
a) \(9{x^2}\left( {2x - 3} \right) = 0\) \(9{x^2} = 0\) hoặc \(2x - 3 = 0\) \({x^2} = 0\) hoặc \(2x = 3\) \(x = 0\) hoặc \(x = \frac{3}{2}\). Vậy phương trình đã cho có hai nghệm là \(x = 0;\) \(x = \frac{3}{2}\). b) Điều kiện xác định \(x \ne - 1,\,\,x \ne 0\). \(\frac{{2x + 1}}{{x + 1}} + \frac{2}{x} = \frac{2}{{x\left( {x + 1} \right)}}\) \(\frac{{\left( {2x + 1} \right)x}}{{x\left( {x + 1} \right)}} + \frac{{2\left( {x + 1} \right)}}{{x\left( {x + 1} \right)}} = \frac{2}{{x\left( {x + 1} \right)}}\) \(\left( {2x + 1} \right)x + 2\left( {x + 1} \right) = 2\) \(2{x^2} + x + 2x + 2 = 2\) \(2{x^2} + 3x = 0\) \(x\left( {2x + 3} \right) = 0\) \(x = 0\) hoặc \(2x + 3 = 0\) \(x = 0\) (không thỏa mãn) hoặc \(x = - \frac{3}{2}\) (thỏa mãn). Vậy nghiệm của phương trình đã cho là \(x = - \frac{3}{2}\). |
c) Ta có: \[4x + 1 < 2x - 9\] \[4x - 2x < - 9 - 1\] \[2x < \; - 10\] \[x < - 5\]. Vậy nghiệm của bất phương trình là \(x < - 5.\) d) \(3\left( {x - 2} \right) + 7x \le 4\left( {x + 1} \right) + 14\) Ta có: \(3x - 6 + 7x \le 4x + 4 + 14\) \(10x - 6 \le 4x + 18\) \(10x - 4x \le 18 + 6\) \(6x \le 24\) \(x \le 4\). Vậy nghiệm của bất phương trình là \(x \le 4\). </></></></></> |
Lời giải
Hướng dẫn giải
Đổi \(1,221{\rm{\;km}} = 1\,\,221{\rm{\;m}}.\)
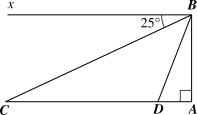
a) Do \[Bx\,{\rm{//}}\,AC\;\] nên \[\widehat {ACB} = \widehat {CBx}\] (so le trong).
Vì \(\Delta ABC\) vuông tại \[A\] nên \(AB = AC \cdot {\rm{tan}}\widehat {ACB} = 1\,\,221 \cdot {\rm{tan}}25^\circ \approx 569{\rm{\;(m)}}{\rm{.}}\)
Vậy chiều cao của đài quan sát khoảng: \[3 + 569 = 572\] (m).
b) Đổi: \[60\] km/h \[ = 1{\rm{ }}000\] m/phút.
Do \[Bx\,{\rm{//}}\,AC\;\] và \[AB \bot AC\] nên ta có \(\widehat {ABx} = \widehat {BAC} = 90^\circ .\)
Quãng đường \[CD\] là: \[CD = 1{\rm{ }}000 \cdot 1 = 1{\rm{ }}000\] (m).
Do đó: \[AD = AC - CD = 1{\rm{ }}221\; - 1{\rm{ }}000 = 221\] (m).
Xét \(\Delta ABD\) vuông tại \[A\] có: \({\rm{tan}}\widehat {ABD} = \frac{{AD}}{{AB}} \approx \frac{{221}}{{569}}.\) Suy ra \(\widehat {ABD} \approx 21^\circ 14'.\)
Mà \(\widehat {DBx} + \widehat {ABD} = \widehat {ABx} = 90^\circ .\)
Suy ra \(\alpha = \widehat {DBx} = 90^\circ - \widehat {ABD} \approx 90^\circ - 21^\circ 14' = 68^\circ 46'.\)
c) Vì \(\Delta ABD\) vuông tại \[A\] nên \(AB = BD \cdot {\rm{cos}}\widehat {ABD}.\)
Suy ra \(BD = \frac{{AB}}{{{\rm{cos}}\widehat {ABD}}} \approx \frac{{569}}{{{\rm{cos}}\,21^\circ 14'}} \approx 610{\rm{\;(m)}}{\rm{.}}\)
Vậy khoảng cách từ mắt người quan sát đến vị trí \[D\] khoảng \[610\] mét.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo