Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M trên tia đối của tia CB lấy điểm N sao cho BM = CN.
Chứng minh rằng tam giác AMN là tam giác cân
Câu hỏi trong đề: Giải toán 7 Chương 2: Tam giác !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
ΔABC cân tại A suy ra 
Ta lại có :
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
| Câu | Đúng | Sai |
|---|---|---|
| 1. Trong một tam giác, góc nhỏ nhất là góc nhọn | ||
| 2. Trong một tam giác có ít nhất là hai góc nhọn | ||
| 3. Trong một tam giác góc lớn nhất là góc tù | ||
| 4. Trong một tam giác vuông , hai góc nhọn bù nhau | ||
| 5. Nếu góc A là góc ở đáy của một tam giác cân thì góc A < 90o | ||
| 6. Nếu góc A là góc ở đỉnh của một tam giác cân thì góc A < 90o |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1. Đúng
2. Đúng
3. Sai. Tam giác nhọn có 3 góc đều nhọn.
4. Sai. Hai góc nhọn phụ nhau.
5. Đúng.
6. Sai. Ví dụ tam giác ABC có 3 góc lần lượt là 120º, 30º, 30º là tam giác cân có góc ở đỉnh bằng 120º.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
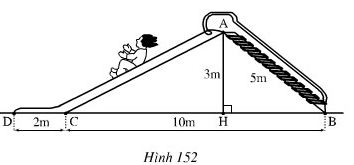
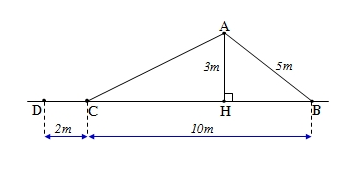
+ ΔAHB vuông tại H
Theo định lí Py–ta- go ta có
HB2 = AB2 – AH2 = 52 – 32 =25 - 9 =16
Suy ra HB = 4 (cm)
Suy ra HC = BC – HB = 10 - 4 = 6(cm)
+ ΔAHC vuông tại H
Theo định lí Py-ta-go ta có
AC2 = AH2 + HC2 = 32 + 62 = 9 + 36 = 45.
Suy ra AC = √45 ≈ 6,7(m)
Độ dài đường trượt ACD bằng: 6,7 + 2= 8,7 (m)
Và hai lần đường lên BA bằng 5.2 =10 (m)
Đo độ dài đường trượt ACD chưa bằng hai lần đườg lên BA
Vậy bạn Mai nói sai, bạn Vân nói đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập
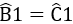
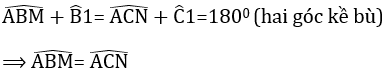
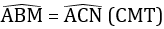
Huyền Thư Ngô
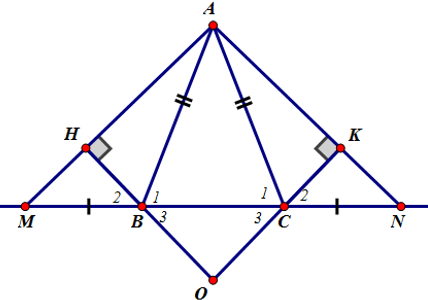
cho tam abc cân tại a. trên tia bc lấy điểm m, trên tia cb lất điểm n, scho bm=cn (m năm giữa b và n). từ b,c lần lượt kẻ bh, ck vuông góc với am, an(h thuộc am, k thuộc an). gọi gia điểm của bh với ck là
a) am=an b)bh=ck c) ap là đường trung trực của bc
Vinguoidanongmanhme
Bài 4. Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M trên tia đối của tia CB lấy điểm N sao cho BM = CN
a) Chứng minh tam giác AMN cân;
b) Kẻ BH vuong goc vs AM (H thuoc AM) kẻ CK vuong goc vs AN (K thuoc AN). Chứng minh tam giac BHM = tam giac CKN
c) Các đường thằng HB và KC cắt nhau tại O. Tam giác OBC là tam giác gì? Tại sao?
d) Khi goc BAC = 60⁰ và BM = CN = BC tính số đo các góc của tam giác AMN và xác định dạng của tam giác OВС.
e) Kẻ AD vuong goc vs BC (D thuoc BC) biết rằng AB = 10cm BC = 16cm Tính độ dài AD.