Cho hình bình hành \[MNPQ\] có tâm \[O.\]
a) \[MN\] song song với \[PQ\] và \[MQ\] song song với \[NP.\]
b) Đoạn thẳng \[OM,{\rm{ }}ON\] lần lượt bằng đoạn thẳng \[OQ,{\rm{ }}OP.\]
c) Góc đỉnh \[M\] bằng góc đỉnh \[P.\]
d) Hình bình hành \[MNPQ\] có hai góc đỉnh \(M,\,\,N\) cùng bằng \(90^\circ \) thì \[MNPQ\] là hình chữ nhật.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: a) Đúng.b) Sai.c) Đúng.d) Đúng.
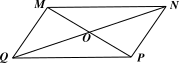
⦁ Vì \[MNPQ\] là hình bình hành nên \[MN\] song song với \[PQ\] và \[MQ\] song song với \[NP.\] Do đó ý a) là đúng.
⦁ Vì hình bình hành \[MNPQ\] có tâm \[O\] nên hai đường chéo \[MP,{\rm{ }}NQ\] cắt nhau tại trung điểm \[O\] của mỗi đường:
\[OM = OP\] và \[ON = OQ.\]
Đoạn thẳng \[OM,{\rm{ }}ON\] lần lượt bằng đoạn thẳng \[OP,{\rm{ }}OQ.\] Do đó ý b) là sai.
⦁ Vì \[MNPQ\] là hình bình hành nên góc đỉnh \[M\] bằng góc đỉnh \[P\] (hai góc đối diện bằng nhau). Do đó ý c) đúng.
⦁ Ta có hình bình hành \[MNPQ\] có góc đỉnh \[M\] bằng góc đỉnh \[P\] và góc đỉnh \[N\] bằng góc đỉnh \[Q\]
Mà hai góc đỉnh \(M,\,\,N\) cùng bằng \(90^\circ \) nên tất cả các góc của hình bình hành \[MNPQ\] đều bằng nhau và bằng \(90^\circ .\) Suy ra \[MNPQ\] là hình chữ nhật. Do đó ý d) đúng.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp số: 11.
Mỗi toa tàu chở được số khách là: \(13 \cdot 7 = 91\) (khách).
Ta có: \(1\,\,000:91 = 10\) dư 90.
Như vậy, cần ít nhất là \(10 + 1 = 11\) toa tàu để chở hết 1 000 khách.
Câu 2
A. \(\left\{ {1;\,\,3;\,\,5;\,\,7} \right\}.\)
B. \(\left\{ {13;\,\,15;\,\,17;\,\,29} \right\}.\)
C. \(\left\{ {3;\,\,5;\,\,7;\,\,51} \right\}.\)
D. \(\left\{ {5;\,\,11;\,\,17;\,\,23} \right\}.\)
Lời giải
Đáp án đúng là: D
Số 1 không phải là số nguyên tố nên phương án A là sai.
Số 15 chia hết cho 3 và 5 nên không phải là số nguyên tố, do đó phương án B là sai.
Số 51 chia hết cho 3 và 17 nên không phải là số nguyên tố, do đó phương án C là sai.
Các số \(5;\,\,11;\,\,17;\,\,23\) chỉ chia hết cho 1 và chính nó nên là số nguyên tố.
Vậy ta chọn phương án D.
Câu 3
A. 10 m.
B. \( - 10\) m.
C. 50 m.
D. \( - 50\) m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(M = \left\{ {7;\,\,8;\,\,9} \right\}.\)
B. \(M = \left\{ {6;\,\,7;\,\,8;\,\,9} \right\}.\)
C. \(M = \left\{ {7;\,\,8;\,\,9;\,\,10} \right\}.\)
D. \(M = \left\{ {6;\,\,7;\,\,8;\,\,9;\,\,10} \right\}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. BCNN của \(a\) và \(b\) là số nhỏ nhất trong tập hợp bội chung của \(a\) và \(b.\)
B. BCNN\(\left( {a,\,\,b,\,\,1} \right) = \)BCNN\(\left( {a,\,\,b} \right).\)
C. Nếu \(m\,\, \vdots \,\,n\) thì BCNN\(\left( {m,\,\,n} \right) = n.\)
D. Nếu ƯCLN\(\left( {x,\,\,y} \right) = 1\) thì BCNN\(\left( {x,\,\,y} \right) = 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\left( {AB + CD} \right) \cdot AD.\)
B. \(\frac{{\left( {AB + CD} \right) \cdot AD}}{2}.\)
C. \(2\left( {AB + CD} \right) \cdot AD.\)
D. \(\frac{{AB \cdot CD \cdot AD}}{2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Tính đối xứng chỉ thể hiện trong Toán học.
B. Tính đối xứng không thể hiện trong Sinh học.
C. Tính đối xứng không thể hiện trong Kiến trúc.
D. Tính đối xứng thể hiện trong Toán học, Tự nhiên, Kiến trúc, Nghệ thuật, Công nghệ chế tạo, ...
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo