Trong các giá trị sau của \[p,\] giá trị nào thoả mãn \[p;\,\,p + 2\] và \[p + 10\] đều là số nguyên tố?
A. \[p = 1\].
B. \[p = 2\].
C. \[p = 3\].
D. \[p = 5\].
Quảng cáo
Trả lời:
Đáp án đúng là: C
Khi \[p = 1\] ta có các số \(1;\,\,3;\,\,11\) nhưng số 1 không phải số nguyên tố.
Khi \[p = 2\] ta có các số \(2;\,\,4;\,\,12\) nhưng số 4 và 12 không phải số nguyên tố.
Khi \[p = 3\] ta có các số \(3;\,\,5;\,\,13\) đều số nguyên tố.
Khi \[p = 5\] ta có các số \(5;\,\,7;\,\,15\) nhưng số 15 không phải số nguyên tố.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Gọi \(x\) (quyển) là số sách mà thư viện cần lưu trữ \(\left( {x \in \mathbb{N}*,\,\,100 \le x \le 150} \right)\).
Nếu xếp thành bó 10 quyển thì thừa 2 quyển nên ta có \[\left( {x - 2} \right)\,\, \vdots \,\,10\] suy ra \[\left( {x - 2 + 10} \right)\,\, \vdots \,\,10\] hay \[\left( {x + 8} \right)\,\, \vdots \,\,10\].
Nếu xếp thành bó 12 quyển thì thừa 4 quyển nên ta có \(\left( {x - 4} \right)\,\, \vdots \,\,12\) suy ra \[\left( {x - 4 + 12} \right)\,\, \vdots \,\,12\] hay \[\left( {x + 8} \right)\,\, \vdots \,\,12\].
Nếu xếp thành bó 15 quyển thì thừa 7 quyển nên ta có \(\left( {x - 7} \right)\,\, \vdots \,\,15\) suy ra \[\left( {x - 7 + 15} \right)\,\, \vdots \,\,15\] hay \[\left( {x + 8} \right)\,\, \vdots \,\,15\].
Do đó \[\left( {x + 8} \right) \in \]BC\(\left( {10,\,\,12,\,\,15} \right)\).
Ta có: \(10 = 2 \cdot 5;\,\,\,\,\,12 = {2^2} \cdot 3;\,\,\,\,\,15 = 3 \cdot 5.\)
Suy ra BCNN\(\left( {10,\,\,12,\,\,15} \right) = {2^2} \cdot 3 \cdot 5 = 60\).
Nên BC\(\left( {10,\,\,12,\,\,15} \right) = \)B\[\left( {60} \right) = \left\{ {0;\,\,60;\,\,120;\,\,180;\,\,240;\,\,300;\,\,...} \right\}\].
Hay \[\left( {x + 8} \right) \in \left\{ {0;\,\,60;\,\,120;\,\,180;\,\,240;\,\,300;\,\,...} \right\}\].
Khi đó \[x \in \left\{ { - 8;\,\,52;\,\,112;\,\,172;\,\,232;\,\,292;\,\,...} \right\}\]
Mà \(100 \le x \le 150\) nên \(x = 112.\)
Vậy thư viện có 112 quyển sách cần lưu trữ.
Lời giải
Hướng dẫn giải
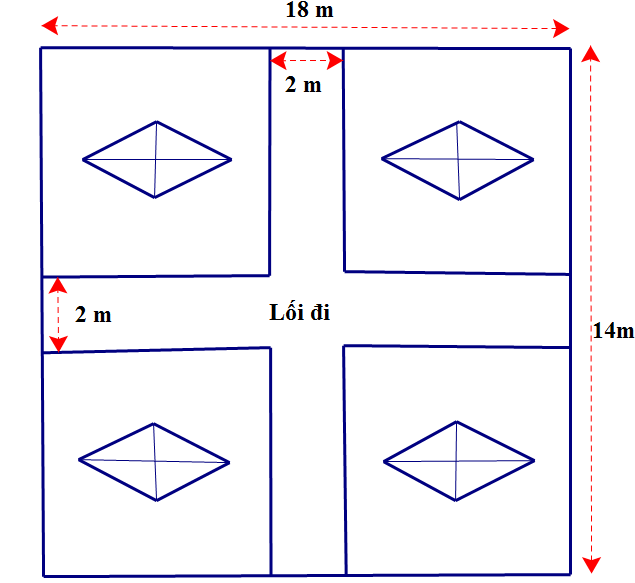
Ở mỗi góc của mảnh đất ban đầu là một ô đất có dạng hình chữ nhật.
Chiều dài của một ô đất ở góc mảnh đất là: \(\left( {18 - 2} \right):2 = 8\) (m).
Chiều rộng của một ô đất ở góc mảnh đất là: \(\left( {14 - 2} \right):2 = 6\) (m).
Diện tích của một ô đất ở góc mảnh đất là: \(8 \cdot 6 = 48\) (m2).
Diện tích đất dùng để làm một bàn tiệc bằng đá dạng hình thoi là: \(\frac{1}{2} \cdot 4 \cdot 3 = 6\) (m2).
Diện tích còn lại trong mỗi ô đất ở góc mảnh đất (sau khi làm bàn tiệc) là: \(48 - 6 = 42\) (m2).
Diện tích dùng để trải thảm cỏ nhân tạo cho cả mảnh đất là: \(4 \cdot 42 = 168\) (m2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(m - 1.\)
B. \(m.\)
C. \(m + 1.\)
D. Không xác định được.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Việt Nam không thuộc tập hợp \(A\).
B. Singapore thuộc tập hợp \(A\).
C. Brunei không thuộc tập hợp \(A\).
D. Nga thuộc tập hợp \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.