(1,0 điểm) Đầu năm học mới, trường THCS A bổ sung vào thư viện nhà trường gần 3 000 quyển sách. Biết rằng nếu xếp mỗi ngăn 26 quyển hoặc 50 quyển hoặc 65 quyển đều thừa 1 quyển, nhưng khi xếp mỗi ngăn 17 quyển thì vừa đủ. Tính số sách mà trường THCS A đã bổ sung.
Câu hỏi trong đề: Bộ 5 đề thi cuối kì 1 Toán 6 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Gọi \(x\) (quyển) là số sách mà trường THCS A bổ sung vào thư viện \(\left( {x \in \mathbb{N}*,\,\,x < 3\,\,000} \right).\)
Nếu xếp mỗi ngăn 26 quyển hoặc 50 quyển hoặc 65 quyển thì đều thừa 1 quyển nên ta có \[x\,\,:\,\,26\] dư 1, \(x\,\,:\,\,50\) dư 1, \(x\,\,:\,\,65\) dư 1.
Do đó \[\left( {x - 1} \right)\,\, \vdots \,\,26,\,\,\left( {x - 1} \right)\,\, \vdots \,\,50,\,\,\left( {x - 1} \right)\,\, \vdots \,\,65.\]
Như vậy, \[\left( {x - 1} \right) \in \]BC\(\left( {26,\,\,50,\,\,65} \right)\).
Ta có: \(26 = 2 \cdot 13;\,\,\,\,\,50 = 2 \cdot {5^2};\,\,\,\,\,65 = 5 \cdot 13.\)
Suy ra BCNN\(\left( {26,\,\,50,\,\,65} \right) = 2 \cdot {5^2} \cdot 13 = 650.\)
Nên BC\(\left( {26,\,\,50,\,\,65} \right) = \)B\[\left( {650} \right) = \left\{ {0;\,\,650;\,\,1\,\,300;\,\,1\,\,950;\,\,2\,\,600;\,\,3\,\,250;\,\,...} \right\}\].
Hay \[\left( {x - 1} \right) \in \left\{ {0;\,\,650;\,\,1\,\,300;\,\,1\,\,950;\,\,2\,\,600;\,\,3\,\,250;\,\,...} \right\}.\]
Khi đó \[x \in \left\{ {1;\,\,651;\,\,1\,\,301;\,\,1\,\,951;\,\,2\,\,601;\,\,3\,\,251;\,\,...} \right\}.\]
Mà \(x < 3\,\,000\) nên \[x \in \left\{ {1;\,\,651;\,\,1\,\,301;\,\,1\,\,951;\,\,2\,\,601} \right\}.\]
Theo bài, khi xếp số sách đó sao cho mỗi ngăn 17 quyển thì vừa đủ nên \(x\,\, \vdots \,\,17\). Trong các số tìm được ở trên, chỉ có số 2 601 chia hết cho 17 nên \(x = 2\,\,601.\)
Vậy trường THCS A đã bổ sung 2 601 quyển sách vào thư viện.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
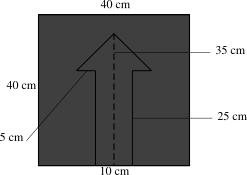
Diện tích biển báo hình vuông là: \({40^2} = 1\,\,600\) (cm2).
Diện tích phần dưới của mũi tên có dạng hình chữ nhật là: \(10 \cdot 20 = 200\) (cm2).
Diện tích phần đầu của mũi tên có dạng hình tam giác là: \(\frac{1}{2} \cdot \left( {5 + 10 + 5} \right) \cdot \left( {35 - 25} \right) = 100\) (cm2).
Diện tích của phần tô đậm trong hình vẽ là: \(1\,\,600 - 200 - 100 = 1\,\,300\) (m2).
Lời giải
Hướng dẫn giải
Đáp án: a) Đúng.b) Sai.c) Đúng.d) Đúng.
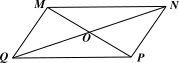
⦁ Vì \[MNPQ\] là hình bình hành nên \[MN\] song song với \[PQ\] và \[MQ\] song song với \[NP.\] Do đó ý a) là đúng.
⦁ Vì hình bình hành \[MNPQ\] có tâm \[O\] nên hai đường chéo \[MP,{\rm{ }}NQ\] cắt nhau tại trung điểm \[O\] của mỗi đường:
\[OM = OP\] và \[ON = OQ.\]
Đoạn thẳng \[OM,{\rm{ }}ON\] lần lượt bằng đoạn thẳng \[OP,{\rm{ }}OQ.\] Do đó ý b) là sai.
⦁ Vì \[MNPQ\] là hình bình hành nên góc đỉnh \[M\] bằng góc đỉnh \[P\] (hai góc đối diện bằng nhau). Do đó ý c) đúng.
⦁ Ta có hình bình hành \[MNPQ\] có góc đỉnh \[M\] bằng góc đỉnh \[P\] và góc đỉnh \[N\] bằng góc đỉnh \[Q\]
Mà hai góc đỉnh \(M,\,\,N\) cùng bằng nên tất cả các góc của hình bình hành 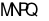 đều bằng nhau và bằng
đều bằng nhau và bằng  Suy ra
Suy ra 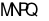 là hình chữ nhật. Do đó ý d) đúng.
là hình chữ nhật. Do đó ý d) đúng.
Câu 3
A. \(m - 1.\)
B. \(m.\)
C. \(m + 1.\)
D. Không xác định được.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(M = \left\{ {7;\,\,8;\,\,9} \right\}.\)
B. \(M = \left\{ {6;\,\,7;\,\,8;\,\,9} \right\}.\)
C. \(M = \left\{ {7;\,\,8;\,\,9;\,\,10} \right\}.\)
D. \(M = \left\{ {6;\,\,7;\,\,8;\,\,9;\,\,10} \right\}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 5 cm.
B. 10 cm.
C. 15 cm.
D. 20 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.