Cho các số nguyên sau: \[-3;\,\,4;\,\,0;\,\,2;\,\,-1;\,\,-5.\]
a) Trong các số trên, số nguyên dương nhỏ nhất là 0.
b) Số \( - 5\) lớn hơn số \( - 3.\)
c) Điểm biểu diễn số đối của số 4 nằm cách điểm 0 bốn đơn vị về bên trái.
d) Sắp xếp các số đối của các số nguyên đã cho theo thứ tự tăng dần là: \[ - 2;\,\, - 4;\,\,0;\,\,1;\,\,3;\,\,5.\]
Câu hỏi trong đề: Bộ 5 đề thi cuối kì 1 Toán 6 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: a) Sai.b) Sai.c) Đúng.d) Sai.
⦁ Vì số 0 không là số nguyên dương, cũng không là số nguyên âm. Mặt khác, trong các số nguyên đã cho, số nguyên dương nhỏ nhất là 2. Do đó ý a) sai.
⦁ Ta có \[--5 < --3.\] Do đó ý b) sai.
⦁ Số đối của số 4 là số \( - 4.\)
Ta có trục số sau:

Quan sát trục số, ta có điểm \( - 4\) cách điểm 0 bốn đơn vị về bên trái. Do đó ý c) đúng.
⦁ Số đối của các số nguyên \[--3;\,\,4;\,\,0;\,\,2;\,\,--1;\,\,--5\] lần lượt là \[3;\,\, - 4;\,0;\,\, - 2;\,\,1;\,\,5.\]
So sánh các số trên, ta được: \[ - 4 < - 2 < 0 < 1 < 3 < 5.\]
Như vậy, sắp xếp các số đối của các số nguyên đã cho theo thứ tự tăng dần ta được \[ - 4;\,\, - 2;\,\,0;\,\,1;\,\,3;\,\,5.\] Do đó ý d) sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
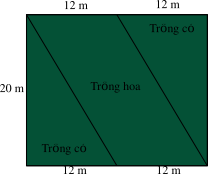
Cách 1: Diện tích mảnh đất hình chữ nhật là: \(24 \cdot 20 = 480\) (m2).
Khu đất dùng để trồng hoa có dạng hình bình hành, do đó diện tích đất dùng để trồng hoa là:
\(12 \cdot 20 = 240\) (m2).
Diện tích dùng để trồng cỏ là: \(480 - 240 = 240\) (m2).
Số tiền cần trả để trồng cỏ là: \(240 \cdot 40\,\,000 = 9\,\,600\,\,000\) (đồng).
Cách 2: Khu đất trồng cỏ được chia làm hai phần bằng nhau có dạng hình tam giác vuông, do đó diện tích trồng cỏ là: \(2 \cdot \left( {\frac{1}{2} \cdot 20 \cdot 12} \right) = 240\) (m2).
Số tiền cần trả để trồng cỏ là: \(240 \cdot 40\,\,000 = 9\,\,600\,\,000\) (đồng).
Lời giải
Hướng dẫn giải
|
a) \[--\left( { - 271} \right)--\left( {531 + 371--731} \right)\] \( = 271--531 - 371 + 731\) \( = \left( {271 - 371} \right) + \left( {--531 + 731} \right)\) \( = \left( { - 100} \right) + 200\) \( = 100.\) |
b) \( - 135 + 45 \cdot 135 + \left( { - 135} \right) \cdot 54\) \( = 135 \cdot \left( { - 1} \right) + 45 \cdot 135 + 135 \cdot \left( { - 54} \right)\) \( = 135 \cdot \left[ {\left( { - 1} \right) + 45 + \left( { - 54} \right)} \right]\) \( = 135 \cdot \left( { - 10} \right)\) \( = - 1350.\) |
Câu 3
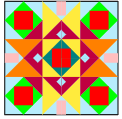
A. Hình vẽ không có tâm đối xứng và có 1 trục đối xứng.
B. Hình vẽ có tâm đối xứng và có 1 trục đối xứng.
C. Hình vẽ có tâm đối xứng và có 2 trục đối xứng.
D. Hình vẽ có tâm đối xứng và có 4 trục đối xứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(2m.\)
B. \(m:2.\)
C. \(m + 2.\)
D. \(m - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.