B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Trong đợt thi đua xây dựng Thư viện số của một trường THCS nhân dịp “Ngày chuyển đổi số quốc gia”, số quyển sách mà ba lớp 7A, 7B, 7C chuyển về dạng video ngắn lần lượt tỉ lệ thuận với \(13;17\) và \(22\). Biết tổng số quyển sách đã chuyển đối của hai lớp 7B và 7C nhiều hơn số quyển sách của lớp 7A là \(78\) quyển. Tính số quyển sách mỗi lớp đã chuyển về dạng video ngắn.
Quảng cáo
Trả lời:
Hướng dẫn giải
Gọi số quyển sách mà mỗi lớp 7A, 7B và 7C đã chuyển về dạng video ngắn là \(x;y;z\) \(\left( {x,y,z \in {\mathbb{N}^*}} \right)\).
Theo đề số sách mà ba lớp 7A, 7B và 7C chuyển về dạng video ngắn lần lượt tỉ lệ thuận với \(13;17\) và \(22\) nên ta có: \(\frac{x}{{13}} = \frac{y}{{17}} = \frac{z}{{22}}\) (1).
Lại có, tổng số quyển sách đã chuyển đổi của hai lớp 7B và 7C nhiều hơn số sách của lớp 7A là \(78\) quyển nên ta có \(y + z - x = 78\) (2).
Từ (1) và (2), áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{13}} = \frac{y}{{17}} = \frac{z}{{22}} = \frac{{y + z - x}}{{17 + 22 - 13}} = \frac{{78}}{{26}} = 3\)
Do đó, \(\frac{x}{{13}} = 3\) nên \(x = 13.3 = 39\) (thỏa mãn)
\(\frac{y}{{17}} = 3\) nên \(y = 17.3 = 51\) (thỏa mãn)
\(\frac{z}{{22}} = 3\) nên \(z = 22.3 = 66\) (thỏa mãn)
Vậy số quyển sách mà mỗi lớp 7A, 7B và 7C chuyển về dạng video ngắn lần lượt là \(39\) quyển, \(51\) quyển, \(66\) quyển.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 (chương trình mới) ( 120.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a)
|
GT |
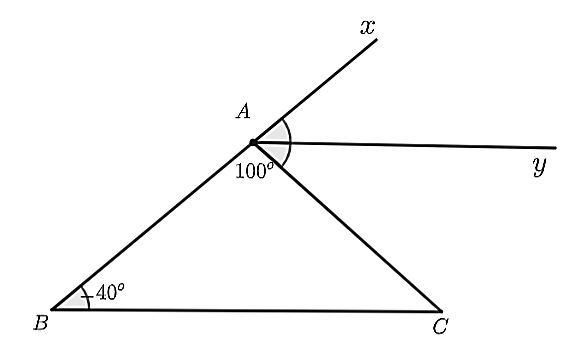
\(\widehat {xBC} = 40^\circ ,\widehat {BAC} = 100^\circ \); \(Ay\) là phân giác của \(\widehat {xAC}\); tia \(Az\) nằm trong \(\widehat {BAC}\); \(\widehat {zAy} = 90^\circ \) |
|
|
KL |
b) \(Ay\parallel BC\). c) tia \(Az\) là phân giác của \(\widehat {BAC}.\) |
b) Nhận thấy \(\widehat {BAC}\) và \(\widehat {CAx}\) là hai góc kề bù.
Do đó, ta có: \(\widehat {BAC} + \widehat {CAx} = 180^\circ \) nên \(\widehat {xAC} = 180^\circ - \widehat {BAC} = 180^\circ - 100^\circ = 80^\circ \).
Lại có \(Ay\) là tia phân giác của \(\widehat {xAC}\) nên \(\widehat {CAy} = \widehat {yAx} = \frac{{\widehat {CAx}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \).
Suy ra \(\widehat {yAx} = \widehat {ABC} = 40^\circ \).
Mà hai góc ở vị trí đồng vị nên \(Ay\parallel BC\).
c)
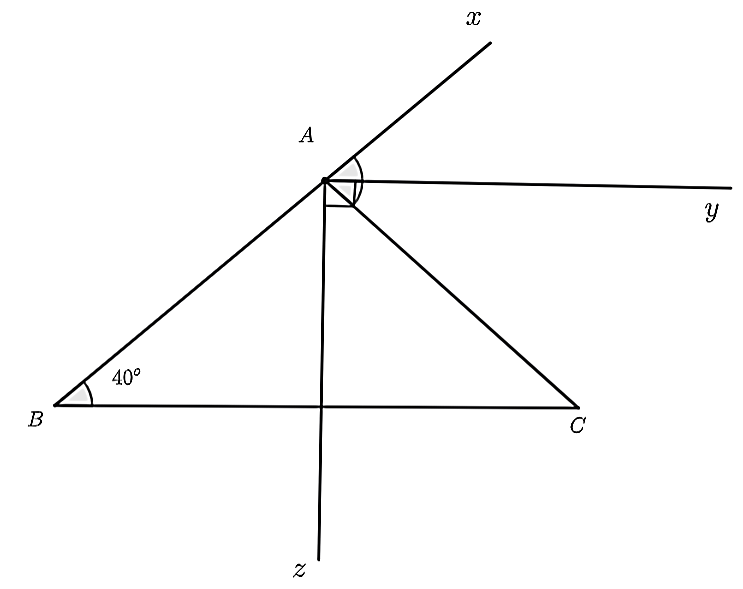
Nhận thấy \(\widehat {yAC}\) và \(\widehat {zAC}\) là hai góc kề nhau nên \(\widehat {zAC} + \widehat {yAC} = \widehat {zAy}\) hay \(\widehat {zAC} + 40^\circ = 90^\circ \).
Suy ra \(\widehat {zAC} = 90^\circ - 40^\circ = 50^\circ \).
Theo đề, tia \(Az\) nằm trong \(\widehat {BAC}\) nên \(\widehat {zAC}\) và \(\widehat {zAB}\) là hai góc kề nhau (1).
Do đó, \(\widehat {zAC} + \widehat {zAB} = \widehat {BAC}\) hay \(50^\circ + \widehat {zAB} = 100^\circ \) suy ra \(\widehat {zAB} = 100^\circ - 50 = 50^\circ \).
Suy ra \(\widehat {zAC} = \widehat {zAB} = 50^\circ \) (2).
Từ (1) và (2) suy ra tia \(Az\) là tia phân giác của \(\widehat {BAC}\).
Lời giải
Hướng dẫn giải
Ta có: \(A = - \frac{1}{3} + \frac{1}{{{3^2}}} - \frac{1}{{{3^3}}} + \frac{1}{{{3^4}}} - \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{100}}}}\)
\(3A = - 1 + \frac{1}{3} - \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} - \frac{1}{{{3^4}}} + ... + \frac{1}{{{3^{99}}}}\)
Suy ra \(3A + A = - 1 + \frac{1}{3} - \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} - \frac{1}{{{3^4}}} + ... + \frac{1}{{{3^{99}}}} + \left( { - \frac{1}{3} + \frac{1}{{{3^2}}} - \frac{1}{{{3^3}}} + \frac{1}{{{3^4}}} - \frac{1}{{{3^5}}} + ... + \frac{1}{{{3^{100}}}}} \right)\)
\(4A = - 1 + \left( {\frac{1}{3} - \frac{1}{3}} \right) + \left( {\frac{1}{{{3^2}}} - \frac{1}{{{3^2}}}} \right) + \left( {\frac{1}{{{3^3}}} - \frac{1}{{{3^3}}}} \right) + \left( {\frac{1}{{{3^4}}} - \frac{1}{{{3^4}}}} \right) + ... + \left( {\frac{1}{{{3^{99}}}} - \frac{1}{{{3^{99}}}}} \right) + \frac{1}{{{3^{100}}}}\)
\(4A = - 1 + \frac{1}{{{3^{100}}}}\)
Suy ra \(A = \frac{1}{4}\left( { - 1 + \frac{1}{{{3^{100}}}}} \right)\).
Do \({3^{100}} > 1\) suy ra \(\frac{1}{{{3^{100}}}} < 1\) nên \(\frac{1}{{{3^{100}}}} - 1 < 0\) suy ra \(\frac{1}{4}\left( { - 1 + \frac{1}{{{3^{100}}}}} \right) < 0\) hay \(A < 0\).
Suy ra \(\left| A \right| = - A\).
Do đó, \(B = 4\left| A \right| + \frac{1}{{{3^{100}}}} = - 4A + \frac{1}{{{3^{100}}}} = - 4.\frac{1}{4}\left( {\frac{1}{{{3^{100}}}} - 1} \right) + \frac{1}{{{3^{100}}}}\)
\( = - \left( {\frac{1}{{{3^{100}}}} - 1} \right) + \frac{1}{{{3^{100}}}} = - \frac{1}{{{3^{100}}}} + 1 + \frac{1}{{{3^{100}}}} = 1 + \left( { - \frac{1}{{{3^{100}}}} + \frac{1}{{{3^{100}}}}} \right) = 1\).
Vậy \(B = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.