(1,0 điểm) Một xe container có thùng hàng dạng hình hộp chữ nhật, kích thước lòng trong thùng hàng dài \(5,8{\rm{ m,}}\) rộng \(3,2{\rm{ m,}}\) cao \(2{\rm{ m}}{\rm{.}}\) Người ta xếp vào thùng container những thùng hàng có dạng hình hộp chữ nhật có chiều dài \(50{\rm{ cm,}}\) chiều rộng \({\rm{40 cm,}}\) chiều cao\(20{\rm{ cm}}{\rm{.}}\) Biết rằng cứ 10 thùng hàng thì xe container nhận được \(5{\rm{ }}000\) đồng tiền công. Tính số thùng hàng có thể chở và tiền công mà xe container nhận được.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Thể tích của lòng trong thùng xe container là: \(5,8.3,2.2 = 37,12{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Thể tích của một thùng hàng là: \(50.40.20 = 40000{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right) = 0,04{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Số thùng hàng xếp được vào thùng xe container là: \(37,12:0,04 = 928\) (thùng hàng).
Số tiền công mà xe container nhận được là: \(\left( {928:10} \right).5{\rm{ }}000 = 464{\rm{ }}000\) (đồng).
Vậy xe container có thể 928 thùng hàng và nhận \(464{\rm{ }}000\) đồng tiền công.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
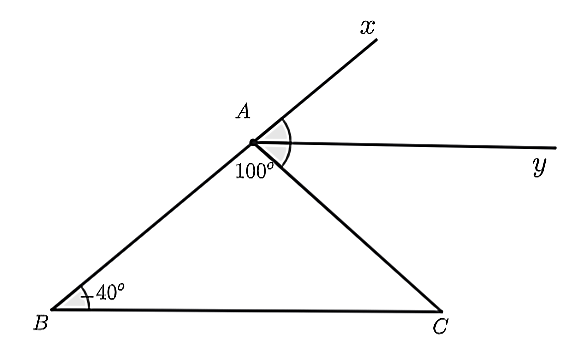
a) Nhận thấy \(\widehat {BAC}\) và \(\widehat {CAx}\) là hai góc kề bù.
Do đó, ta có: \(\widehat {BAC} + \widehat {CAx} = 180^\circ \) nên \(\widehat {xAC} = 180^\circ - \widehat {BAC} = 180^\circ - 100^\circ = 80^\circ \).
Lại có \(Ay\) là tia phân giác của \(\widehat {xAC}\) nên \(\widehat {CAy} = \widehat {yAx} = \frac{{\widehat {CAx}}}{2} = \frac{{80^\circ }}{2} = 40^\circ \).
Suy ra \(\widehat {yAx} = \widehat {ABC} = 40^\circ \).
Mà hai góc ở vị trí đồng vị nên \(Ay\parallel BC\).
b)
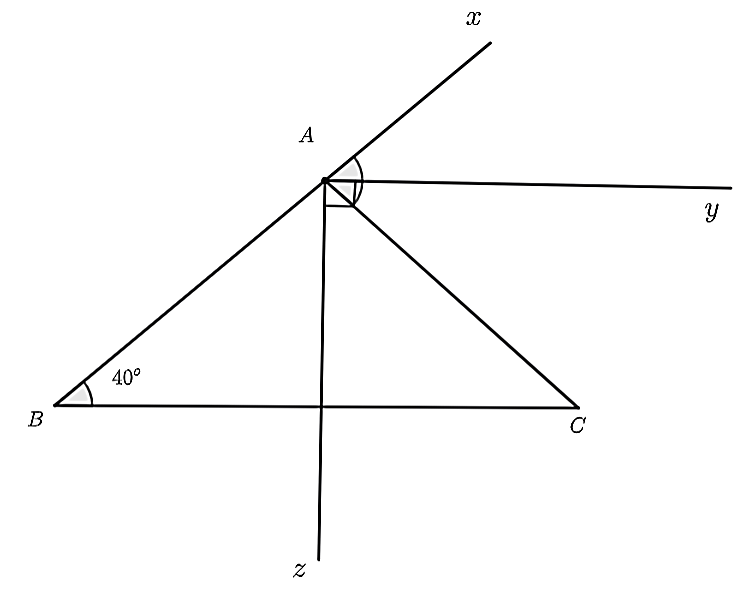
Vì tia \(Az\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAz} = \widehat {zAC} = \widehat {\frac{{BAC}}{2}} = \frac{{100^\circ }}{2} = 50^\circ \).
Nhận thấy \(\widehat {yAC}\) và \(\widehat {zAC}\) là hai góc kề nhau nên \(\widehat {zAC} + \widehat {yAC} = \widehat {zAy}\) .
Suy ra \(\widehat {zAy} = 40^\circ + 50^\circ = 90^\circ \).
Do đó, \(Az \bot Ay\).
Lời giải
Đáp án đúng là: D
Ta có: \(\sqrt {0,04} = \sqrt {{{\left( {0,2} \right)}^2}} = 0,2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo