B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Thực hiện phép tính:
a) \(27\frac{1}{5}:\frac{8}{3} - 51\frac{1}{5}.\frac{3}{8} + 19\);
b) \(25.{\left( { - \frac{1}{2}} \right)^2} - 2.{\left( { - \frac{1}{2}} \right)^2} - 3.\sqrt {\frac{1}{{16}}} \).
Quảng cáo
Trả lời:
Hướng dẫn giải
|
a) \(27\frac{1}{5}:\frac{8}{3} - 51\frac{1}{5}.\frac{3}{8} + 19\) \( = 27\frac{1}{5}.\frac{3}{8} - 51\frac{1}{5}.\frac{3}{8} + 19\) \( = \left( {27\frac{1}{5} - 51\frac{1}{5}} \right).\frac{3}{8} + 19\) \( = - 24.\frac{3}{8} + 19\) \( = - 9 + 19\) \( = 10.\) |
b) \(25.{\left( { - \frac{1}{2}} \right)^2} - 2.{\left( { - \frac{1}{2}} \right)^2} - 3.\sqrt {\frac{1}{{16}}} \) \( = 25.\frac{1}{4} - 2.\frac{1}{4} - 3.\sqrt {{{\left( {\frac{1}{4}} \right)}^2}} \) \( = 25.\frac{1}{4} - 2.\frac{1}{4} - 3.\frac{1}{4}\) \( = \left( {25 - 2 - 3} \right).\frac{1}{4}\) \( = 20.\frac{1}{4}\) \( = 5.\) |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
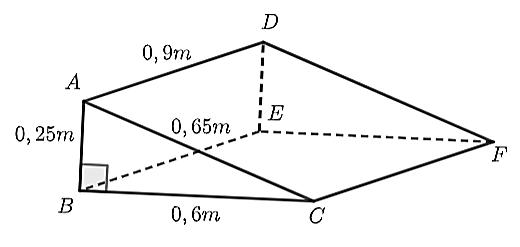
Diện tích xung quanh của cái gờ là: \(\left( {0,25 + 0,6 + 0,65} \right).0,9 = 1,35\) (m2).
Diện tích hai mặt đáy của cái gờ đó là: \(2.\frac{1}{2}.0,25,0,6 = 0,15\) (m2).
Diện tích cần sơn của cái gờ đó là: \(1,35 + 0,15 = 1,5\) (m2).
Số tiền cần để quét vôi tất cả các mặt của gờ đó là: \(300{\rm{ 000}}{\rm{.1,5 = 450 000}}\) (đồng).
Vậy ông An cần trả \({\rm{450 000}}\) đồng để sơn tất cả các mặt của cái gờ.
Lời giải
Hướng dẫn giải
Đáp án: \(35\)
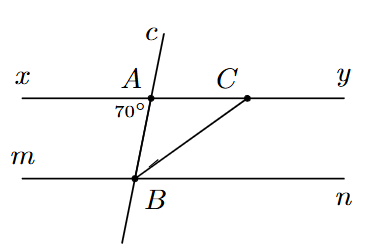
Vì
\(xy\parallel mn\) nên \(\widehat {xAB} = \widehat {ABn} = 70^\circ \) (so le trong).
Ta có tia \(BC\) là tia phân giác của \(\widehat {ABn}\) nên \(\widehat {ABC} = \widehat {CBn} = \widehat {\frac{{ABn}}{2}} = 35^\circ \).
Vì \(xy\parallel mn\) nên \(\widehat {ACB} = \widehat {CBn} = 35^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Đều có 6 măt.
B. Đều có 8 đỉnh.
C. Các mặt đáy song song với nhau.
D. Mỗi đỉnh có 3 góc vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.