Cho tứ giác \(MNPQ\) có \(PM\) là tia phân giác của góc \(\widehat {NPQ}.\) Biết \(\widehat {QMN} = 110^\circ ,\) \(\widehat {N\,} = 120^\circ \) và \(\widehat {Q\,} = 60^\circ .\) Tính số đo của \(\widehat {MPQ}\) (đơn vị: độ).
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp số: 35.
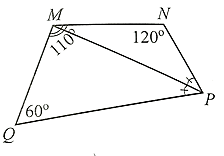
Xét tứ giác \[MNPQ,\] ta có: \(\widehat Q + \widehat {QMN} + \widehat N + \widehat {NPQ} = 360^\circ \) (tổng các góc của một tứ giác).
Suy ra \(\widehat {NPQ} = 360^\circ - \left( {\widehat {QMN} + \widehat N + \widehat Q} \right) = 360^\circ - \left( {110^\circ + 120^\circ + 60^\circ } \right) = 70^\circ \).
Do \[PM\] là tia phân giác của góc \[NPQ\] nên ta có: \(\widehat {MPQ} = \frac{{\widehat {NPQ}}}{2} = \frac{{70^\circ }}{2} = 35^\circ \).
Vậy số đo của \(\widehat {MPQ}\) là \(35^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp số: \[ - {\bf{216}}\].
Ta có \(M = {\left( {x + 3} \right)^3} - \left( {x + 9} \right)\left( {{x^2} + 27} \right)\)
\[ = {x^3} + 9{x^2} + 27x - 27 - \left( {{x^3} + 27x + 9{x^2} + 243} \right)\]
\( = {x^3} + 9{x^2} + 27x + 27 - {x^3} - 27x - 9{x^2} - 243\)
\( = \left( {{x^3} - {x^3}} \right) + \left( {9{x^2} - 9{x^2}} \right) + \left( {27x - 27x} \right) - \left( {243 - 27} \right)\)\( = - 216\).
Vậy \(M = - 216.\)
Lời giải
Ta có \(2{x^2}y{\left( {2{y^3}} \right)^2} = 2{x^2}y \cdot 4{y^6} = 8{x^2}{y^7}.\)
Đơn thức trên có bậc là \(2 + 7 = 9.\)
Vậy đơn thức \(2{x^2}y{\left( {2{y^3}} \right)^2}\) có bậc là 9.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Dữ liệu số rời rạc.
B. Dữ liệu không là số có thể sắp thứ tự.
C. Dữ liệu số liên tục.
D. Dữ liệu không là số không thể sắp thứ tự.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(35,6\% \).
B. \(52,5\% \).
C. \(32,5\% \).
D. \(61,9\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.