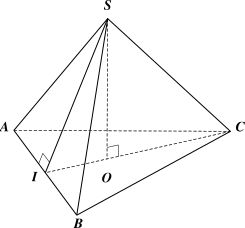
Cho tam giác \[ABC\]. Dựng bên ngoài tam giác đó hai tam giác \[ABD,{\rm{ }}ACE\] vuông cân tại đỉnh \[A\] rồi dựng hình bình hành \[AEID\]. Biết \[\widehat {DAI} = \widehat {ABC}\]. Gọi \[K\] là trung điểm của \[BD.\]
a) \[\widehat {DAI} + \widehat {BAH} = 45^\circ \].
b) \[AI \bot BC\].
c) \(\widehat {EBA} = \widehat {CDA}\).
d) \[KA = \frac{1}{2}KB\].
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án:
a) Sai.
b) Đúng.
c) Đúng.
d) Sai.
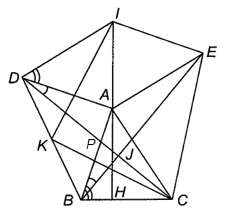
⦁ Giả sử \[AI\] cắt \[BC\] ở \[H\].
Ta có: \[\widehat {DAI} + \widehat {DAB} + \widehat {BAH} = 180^\circ \], mà \[\widehat {DAB} = 90^\circ \] (do \[\Delta DAB\] vuông cân tại \[A\]).
Suy ra \[\widehat {DAI} + \widehat {BAH} = 90^\circ \]. Do đó ý a) sai.
⦁ Ta có \[\widehat {DAI} = \widehat {ABC}\] (gt) nên \[\widehat {ABH} + \widehat {BAH} = 90^\circ \].
Trong \[\Delta ABH\] có: \[\widehat {ABH} + \widehat {BAH} + \widehat {AHB} = 180^\circ \].
Suy ra \[\widehat {AHB} = 180^\circ \left( {\widehat {ABH} + \widehat {BAH}} \right) = 180^\circ - 90^\circ = 90^\circ \] hay \[AI \bot BC\]. Do đó ý b) đúng.
⦁ Ta có \[\widehat {BAE} = \widehat {BAC} + \widehat {CAE} = \widehat {BAC} + 90^\circ \] và \[\widehat {DAC} = \widehat {BAC} + \widehat {BAD} = \widehat {BAC} + 90^\circ \].
Do đó \[\widehat {BAE} = \widehat {DAC}\].
Xét \[\Delta BAE\] và \[\Delta DAC\] có:
\[AB = AD;\,\,\widehat {BAE} = \widehat {DAC};\,\,AC = AE\];
Do đó \[\Delta BAE = \Delta DAC\] (c.g.c).
Suy ra \(\widehat {EBA} = \widehat {CDA}\) (hai góc tương ứng). Do đó ý c) đúng.
⦁ Tam giác \[ABD\] vuông cân tại \[A\] nên \[AK\] vừa là đường trung tuyến, vừa là đường cao, đường phân giác. Do đó \(\widehat {DAK} = \frac{1}{2}\widehat {BAD} = 45^\circ \).
Khi đó \(\widehat {ABK} = \widehat {BAK} = 45^\circ \) nên \[\Delta ABK\] vuông cân tại \[K\], do đó \[KA = KB\]. Do đó ý d) sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
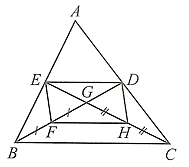
a) Tam giác \[ABC\] có các đường trung tuyến \[BD,{\rm{ }}CE\] cắt nhau tại \[G\] nên \[G\] là trọng tâm \[\Delta ABC,\] do đó \(DG = \frac{1}{2}BG,\) \(EG = \frac{1}{2}CG.\)
Mà \[F,{\rm{ }}H\] lần lượt là trung điểm của \[BG,{\rm{ }}CG\] nên
\(BF = FG = \frac{1}{2}BG,\) \(CH = HG = \frac{1}{2}CG.\)
Do đó \[DG = BF = FG,{\rm{ }}EG = CH = HG.\]
Suy ra, \[G\] là trung điểm của \[FD,{\rm{ }}G\] là trung điểm của \[EH.\]
Tứ giác \[EFHD\] có hai đường chéo \[EH\] và \(FD\) cắt nhau tại trung điểm \[G\] của mỗi đường nên \[EFHD\] là hình bình hành.
b) Để hình bình hành \[EFHD\] là hình vuông thì \[EH = DF\] và \[EH \bot DF.\]
Suy ra \[EG = DG,{\rm{ }}BG = CG\] và \[BD \bot CE.\]
⦁ Xét \(\Delta BEG\) và \[\Delta CDG\] có:
\[BG = CG,\] \(\widehat {EGB} = \widehat {DGC}\) (đối đỉnh), \[EG = DG\]
Do đó \(\Delta BEG = \Delta CDG\) (c.g.c).
Suy ra \[BE = CD\] (hai cạnh tương ứng).\[\left( 1 \right)\]
Mà \[BD,{\rm{ }}CE\] là các đường trung tuyến của \(\Delta ABC\) nên \[E\] là trung điểm của \[AB,{\rm{ }}D\] là trung điểm của \[AC.\]
Suy ra \[AB = 2BE,{\rm{ }}AC = 2CD.\,\,\,\,\,\,\left( 2 \right)\]
Từ (1) và (2) suy ra \[AB = AC.\]
⦁ Dễ thấy, nếu \[AB = AC\] và \[BD \bot CE\] thì tứ giác \[EFHD\] là hình vuông.
Vậy tam giác \[ABC\] cân tại \[A\] có hai đường trung tuyến \[BD,CE\] vuông góc với nhau thì tứ giác \[EFHD\] là hình vuông.
Câu 2
A. Biểu đồ đoạn thẳng.
B. Biểu đồ cột kép.
C. Biểu đồ tranh.
D. Biểu đồ hình quạt tròn.
Lời giải
Khi muốn biểu diễn tuổi thọ trung bình của người Việt Nam qua 40 năm thì nên lựa chọn biểu đồ đoạn thẳng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[92,25\% \].
B. \(52,25\% \).
C. \(7,75\% \).
D. \(72,75\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.