Câu hỏi:
12/07/2024 5,057Một cách chứng minh khác của định lí 2:
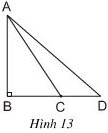
Cho hình 13. Dùng quan hệ giữa góc và cạnh đối diện trong một tam giác để chứng minh rằng:
Nếu BC < BD thì AC < AD
Trong tam giác ACD, cạnh nào lớn nhất, tại sao?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trong tam giác ACD có góc ACD là góc tù .
Mà AD là cạnh đối diện với góc ACD.
⇒ AD là cạnh lớn nhất trong tam giác ACD (cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác).
nên AD > AC hay AC < AD
Vậy Nếu : BC < BD thì AC < AD.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
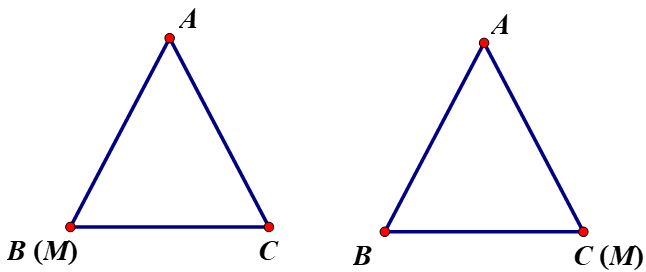
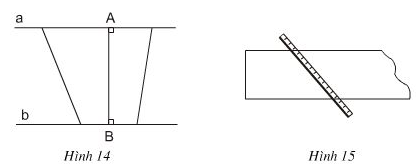
Giả sử ΔABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB; AM ≤ AC.
- TH1 : Nếu M ≡ B hoặc M ≡ C (Kí hiệu đọc là trùng với) thì AM = AB = AC.
- TH2 : Nếu M nằm giữa B và C và M ≠ B; M ≠ C.
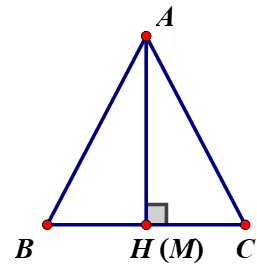
Kẻ AH ⊥ BC tại H
+ Nếu M ≡ H ⇒ AM ⊥ BC tại M hay AM là đường vuông góc từ A đến BC.
Mà AB, AC là các đường xiên từ A đến đường thẳng BC.
Theo định lí 1 : Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường thẳng vuông góc là đường ngắn nhất.
⇒ AM < AB và AM < AC.
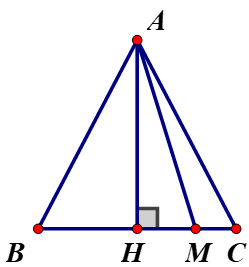
+ Nếu M ≠ H giả sử M nằm giữa H và C ⇒ MH < CH.
Vì MH và CH lần lượt là hình chiếu của đường xiên MA và CA trên đường BC
Mà MH < CH ⇒ MA < CA (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
Chứng minh tương tự nếu M nằm giữa H và B
Vậy mọi vị trí của M trên cạnh đáy BC thì AM ≤ AB = AC.
Lời giải
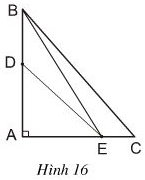
Trong hình vẽ D nằm giữa A và B ⇒ AD < AB
Ta có: ED, EB là hai đường xiên vẽ từ E đến đường AB
EA ⏊ AB tại A nên A là hình chiếu của E trên AB.
⇒ AD, AB lần lượt là hình chiếu của ED, EB trên AB
Trong hình vẽ D nằm giữa A và B ⇒ AD < AB nên ED < EB hay DE < BE (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
Kết hợp với kết quả câu a suy ra DE < BE < BC ⇒ DE < BC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2
Nhắn tin Zalo