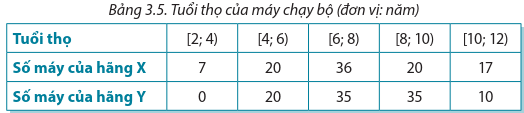
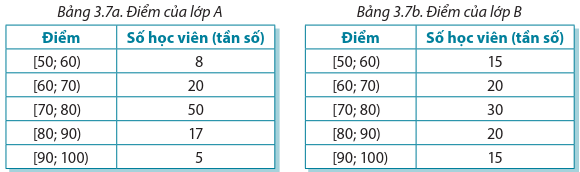
Bảng 3.3 biểu thị kết quả điều tra thời gian sử dụng Internet hằng ngày của một số người.

Tìm khoảng biến thiên của mẫu số liệu đã cho. Kết quả cho biết điều gì?
Bảng 3.3 biểu thị kết quả điều tra thời gian sử dụng Internet hằng ngày của một số người.

Tìm khoảng biến thiên của mẫu số liệu đã cho. Kết quả cho biết điều gì?
Câu hỏi trong đề: 15 bài tập Khoảng biến thiên (có lời giải) !!
Quảng cáo
Trả lời:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Cỡ mẫu là \(n = 3 + 12 + 15 + 8 = 38\). Gọi \({x_1}, \ldots ,{x_{38}}\) là thời gian chờ khám bệnh của 38 bệnh nhân này và giả sử rằng dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{10}}\) nên nhóm chứa tứ phân vị thứ nhất là nhóm \([5;10)\) và ta có: \({Q_1} = 5 + \left[ {\frac{{\frac{{38}}{4} - 3}}{{12}}} \right] \cdot 5 \approx 7,71\)
Tứ phân vị thứ ba của mã̃u số liệu gốc là \({x_{29}}\) nên nhóm chứa tứ phân vị thứ ba là nhóm [10 ; 15) và ta có: \({Q_3} = 10 + \left[ {\frac{{\frac{{3 \cdot 38}}{4} - 15}}{{15}}} \right] \cdot 5 = 14,5\)
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} \approx 14,5 - 7,71 = 6,79\).
b) Do \({\Delta _Q} = 6,79 < 9,23\) nên thời gian chờ của bệnh nhân tại phòng khám \(Y\) phân tán hơn thời gian chờ của bệnh nhân tại phòng khám \(X\).
Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.