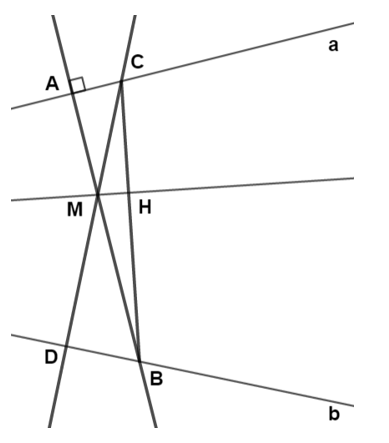
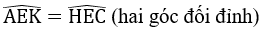Cho hình 66. Không vẽ giao điểm của a, b, hãy nêu cách vẽ đường thẳng đi qua giao điểm này và điểm M.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Áp dụng kết quả bài tập 69 (chương III – SGK) ta có cách vẽ sau:
- Vẽ đường thẳng d qua M và vuông góc với a.
- Vẽ đường thẳng l qua M và vuông góc với b.
- d cắt a, b lần lượt tại A và B.
- l cắt a, b lần lượt tại C và D.
- Vẽ đường thẳng c qua M vuông góc với BC
⇒ c là đường qua M và qua giao điểm của hai đường a, b
Chứng minh:
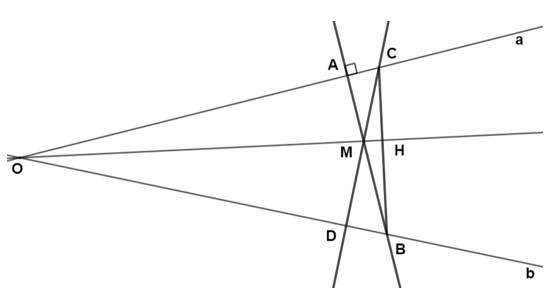
Giả sử a cắt b tại điểm O.
Khi đó BA, DC là hai đường cao của ∆OBC.
Mà BA và DC cắt nhau tại M nên M là trực tâm ∆OBC.
Do đó OM cũng là đường cao nên OM ⟘ BC hay đường thẳng qua M vuông góc với BD thì đi qua O.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
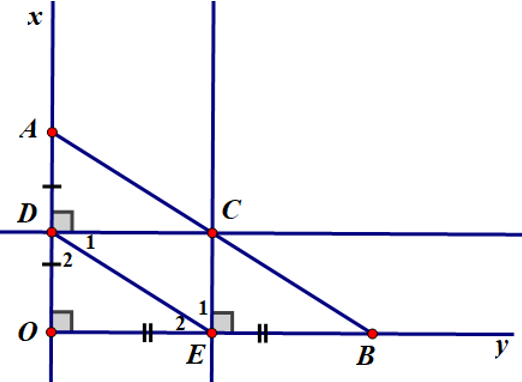
Xét ΔAEK vuông tại A và ΔHEC vuông tại H có:
AE = EH (chứng minh trên)
⇒ ΔAEK = ΔHEC (cạnh góc vuông – góc nhọn kề)
⇒ EK = EC (hai cạnh tương ứng)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo