Bạn An ném một quả bóng cao su có khối lượng \(0,15{\rm{\;kg}}\) xuống sàn theo phương thẳng đứng, sau khi va chạm với sàn, quả bóng nảy lên theo phương thẳng đứng. Tốc độ của quả bóng ngay trước khi va chạm là \(6,50{\rm{\;m/s}}\) và ngay sau va chạm là \(6,25{\rm{\;m/s}}\). Biết rằng, thời gian quả bóng tiếp xúc với sàn là \({0,25.10^{ - 1}}s\) thì độ lớn của lực trung bình mà sàn tác dụng lên quả bóng là
Bạn An ném một quả bóng cao su có khối lượng \(0,15{\rm{\;kg}}\) xuống sàn theo phương thẳng đứng, sau khi va chạm với sàn, quả bóng nảy lên theo phương thẳng đứng. Tốc độ của quả bóng ngay trước khi va chạm là \(6,50{\rm{\;m/s}}\) và ngay sau va chạm là \(6,25{\rm{\;m/s}}\). Biết rằng, thời gian quả bóng tiếp xúc với sàn là \({0,25.10^{ - 1}}s\) thì độ lớn của lực trung bình mà sàn tác dụng lên quả bóng là
A. \(76,5{\rm{\;N}}\).
B. \(1,5{\rm{\;N}}\).
C. \(3400,0{\rm{\;N}}\).
D. \(66,7{\rm{\;N}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
Sử dụng định luật Newton II để xác định lực tác dụng: F = ma
Áp dụng công thức tính gia tốc: \(a = \frac{{{\rm{\Delta }}v}}{{{\rm{\Delta }}t}}\)
Cách giải:
Chọn chiều dương là chiều từ trên xuống dưới.
Gọi vận tốc ngay trước khi va chạm là \({\vec v_1}\) và ngay sau va chạm là \(\overrightarrow {{v_2}} \)
Trong quá trình va chạm ta có: \(\overrightarrow {{v_1}} \) hướng xuống và \(\overrightarrow {{v_2}} \) hướng lên.
Độ biến thiên vận tốc của vật là:
\(\left| {{\rm{\Delta }}v} \right| = \left| {{v_2} - {v_1}} \right| = \left| { - 6,25 - 6,50} \right| = 12,75{\rm{\;m}}/{\rm{s}}\)
Áp dụng công thức định luật II Newton ta có lực tác dụng:
\(\left| F \right| = m\left| a \right| = m.\frac{{\left| {{\rm{\Delta }}v} \right|}}{{{\rm{\Delta }}t}} = 0,15.\frac{{12,75}}{{{{0,25.10}^{ - 1}}}} = 76,5\left( {\rm{N}} \right)\)
Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
+ Phân tích đồ thị kết hợp với nhớ lại khái niệm các đẳng quá trình.
+ Áp dụng biểu thức của các đẳng quá trình để tìm các thông số chưa biết.
+ Sử dụng công thức: \({\rm{\Delta }}U = \frac{3}{2}nR{\rm{\Delta }}T\)
Cách giải:
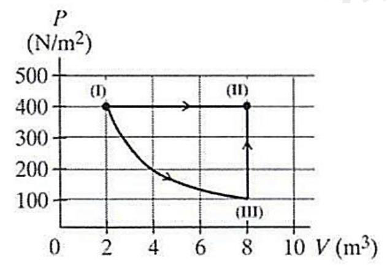
a) Từ đồ thị ta thấy quá trình \({\rm{A}}\left( {{\rm{I}} \to {\rm{II}}} \right)\): áp suất \(p = 400\left( {{\rm{N}}/{{\rm{m}}^2}} \right)\) không đổi
\( \to \) Quá trình A là quá trình đẳng áp.
\( \to \) a đúng.
b) Quá trình B gồm 2 quá trình:
+ \({\rm{I}} \to \) III: \({p_I}{V_I} = {p_{III}}{V_{II}} \to \) quá trình đẳng nhiệt
+ \({\rm{III}} \to {\rm{II}}:{V_{{\rm{III\;}}}} = {V_{II}} = 8{\rm{\;}}{{\rm{m}}^3} \to \) quá trình đẳng tích
\( \to \) b sai.
c) Biến thiên nội năng: \({\rm{\Delta }}U = \frac{3}{2}nR{\rm{\Delta }}T\) (chỉ phụ thuộc vào nhiệt độ).
Mà quá trình A và B có trạng thái đầu và cuối giống nhau nên sự biến thiên nội năng của hệ trong hai quá trình này bằng nhau.
\( \to \) c sai.
d) Trạng thái (I): \(\left\{ {\begin{array}{*{20}{l}}{{p_I} = 400\left( {{\rm{N}}/{{\rm{m}}^2}} \right)}\\{{V_I} = 2{\rm{\;}}{{\rm{m}}^3}}\\{{T_1} = T}\end{array}} \right.\)
Ta có: \(\frac{{{V_I}}}{{{T_I}}} = \frac{{{V_{II}}}}{{{T_{II}}}} \Leftrightarrow {T_{II}} = \frac{{{V_{II}}{T_I}}}{{{V_I}}} = \frac{{8.T}}{2} = 4T\)
Biến thiên nội năng của hệ trong quá trình \(B\) là:
\({\rm{\Delta }}U = \frac{3}{2}nR{\rm{\Delta }}T = \frac{3}{2}.nR\left( {{T_2} - {T_1}} \right) = \frac{3}{2}nR\left( {4T - T} \right) = \frac{9}{2}nRT\)
\( \Rightarrow {\rm{\Delta }}U = \frac{9}{2}{p_I}{V_I} = \frac{9}{2}.400.2 = 3600{\rm{\;J}}\)
\( \to \) d đúng.
Lời giải
Phương pháp:
Vật chuyển động thẳng đều khi tổng hợp lực tác dụng lên vật bằng 0
Lực từ: \(F = IBl{\rm{sin}}\alpha \)
Từ thông: \({\rm{\Phi }} = BS{\rm{cos}}\alpha \)
Suất điện động cảm ứng: \({e_c} = - \frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}\)
Cường độ dòng điện cảm ứng: \({I_c} = \frac{{{e_c}}}{R}\)
Cách giải:
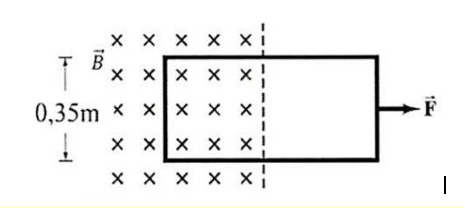
Độ dịch chuyển của khung dây là: \({\rm{d}} = {\rm{vt}}\)
Diện tích khung dây trong từ trường biến thiên một lượng:
\({\rm{\Delta }}S = d.0,35 = 0,35vt\)
Suất điện động cảm ứng trong khung dây có độ lớn là:
\({e_c} = B.\left| {\frac{{{\rm{\Delta }}S}}{t}} \right| = B.\left| {\frac{{0,35vt}}{t}} \right| = 0,35Bv\)
Cường độ dòng điện cảm ứng là:
\({I_c} = \frac{{{e_c}}}{R} = \frac{{0,35Bv}}{R}\)
Cường độ dòng điện cảm ứng trong khung dây, phần khung dây trong từ trường chịu tác dụng của lực từ, lực từ này có tác dụng chống lại sự dịch chuyển của khung dây, cân bằng với lực kéo F
Độ lớn của lực kéo bằng độ lớn của lực từ:
\(F = {I_c}B.0,35 = \frac{{0,35Bv}}{R}.0,35B = \frac{{{{0,35}^2}{B^2}v}}{R}\)
\( \Rightarrow F = \frac{{{{0,35}^2}{{.0,55}^2}.3,1}}{{0,25}} \approx 0,5\left( {\rm{N}} \right)\)
Đáp số: 0,5
Câu 3
A. khối lượng của các phân tử tăng lên.
B. khối lượng của các phân tử giảm xuống.
C. nội năng trung bình của các phân tử khí tăng lên.
D. nội năng trung bình của các phân tử khí giảm xuống.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \({25^ \circ }{\rm{C}}\).
B. \({100^ \circ }{\rm{C}}\).
C. Không xác định được.
D. \({115^ \circ }{\rm{C}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập