Trong một ống tia điện tử, người ta tạo ra một chùm tia electron nhờ điện áp tăng tốc bằng \({\rm{U}} = 2,70{\rm{kV}}\). Sau đó chùm tia electron đi qua vùng có tác dụng của từ trường hoặc vùng có tác dụng của điện trường.
- Thí nghiệm 1: cho chùm electron đi qua vùng điện trường đều \(\vec E\) nằm trong mặt phẳng hình vẽ, hướng lên trên hoặc xuống dưới. Đồ thị mô tả đường đi của electron (từ bên trái) bị lệch về phía dưới (Hình a)
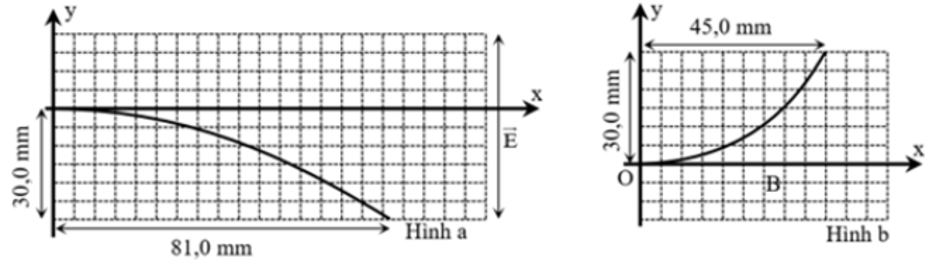
- Thí nghiệm 2: cho chùm electron đi qua vùng từ trường đều \(\vec B\) có phương vuông góc với mặt phẳng hình vẽ, electron có đường đi như hình \(b\). Biết lực từ tác dụng lên electron có phương vuông góc với vectơ cảm ứng từ \(\vec B\) và với vận tốc \(\vec v\) của hạt, chiều xác định theo quy tắc bàn tay trái, có độ lớn \(f = Bv\left| q \right|\). Bỏ qua tác dụng của trọng trường, tốc độ của electron trước khi tăng tốc.
a) Tốc độ của electron trước khi đi vào vùng điện trường hoặc từ trường bằng \({3,08.10^7}{\rm{\;m}}/{\rm{s}}\).
b) Cường độ điện trường \(\vec E\) ngược hướng với \(\overrightarrow {Oy} \). Quỹ đạo của electron mô tả ở hình a là một cung parabol.
c) Cảm ứng từ \(\vec B\) đi ra khỏi mặt phẳng hình vẽ. Quỹ đạo của electron mô tả ở hình b là một cung parabol.
d) Để chùm electron không bị lệch khỏi phương ban đầu khi đặt đồng thời điện trường và từ trường trên thì điện áp U phải có giá trị bằng 539 V.
Trong một ống tia điện tử, người ta tạo ra một chùm tia electron nhờ điện áp tăng tốc bằng \({\rm{U}} = 2,70{\rm{kV}}\). Sau đó chùm tia electron đi qua vùng có tác dụng của từ trường hoặc vùng có tác dụng của điện trường.
- Thí nghiệm 1: cho chùm electron đi qua vùng điện trường đều \(\vec E\) nằm trong mặt phẳng hình vẽ, hướng lên trên hoặc xuống dưới. Đồ thị mô tả đường đi của electron (từ bên trái) bị lệch về phía dưới (Hình a)
- Thí nghiệm 2: cho chùm electron đi qua vùng từ trường đều \(\vec B\) có phương vuông góc với mặt phẳng hình vẽ, electron có đường đi như hình \(b\). Biết lực từ tác dụng lên electron có phương vuông góc với vectơ cảm ứng từ \(\vec B\) và với vận tốc \(\vec v\) của hạt, chiều xác định theo quy tắc bàn tay trái, có độ lớn \(f = Bv\left| q \right|\). Bỏ qua tác dụng của trọng trường, tốc độ của electron trước khi tăng tốc.
a) Tốc độ của electron trước khi đi vào vùng điện trường hoặc từ trường bằng \({3,08.10^7}{\rm{\;m}}/{\rm{s}}\).
b) Cường độ điện trường \(\vec E\) ngược hướng với \(\overrightarrow {Oy} \). Quỹ đạo của electron mô tả ở hình a là một cung parabol.
c) Cảm ứng từ \(\vec B\) đi ra khỏi mặt phẳng hình vẽ. Quỹ đạo của electron mô tả ở hình b là một cung parabol.
d) Để chùm electron không bị lệch khỏi phương ban đầu khi đặt đồng thời điện trường và từ trường trên thì điện áp U phải có giá trị bằng 539 V.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
- Định lý biến thiên động năng: \({\rm{\Delta }}{{\rm{W}}_d} = A \Rightarrow \frac{1}{2}m\left( {{v^2} - v_0^2} \right) = qU\)
- Áp dụng định luật II Newton: \(\vec F = m\vec a\)
- Công thức của chuyển động thẳng biến đổi đều: \(y = {v_0}t + \frac{1}{2}a{t^2}\)
- Lực điện tác dụng lên điện tích: \(\vec F = q\vec E\)
- Để chùm e không bị lệch khỏi phương ban đầu thì lực điện phải cân bằng với lực từ: \(\left| q \right|E = \left| q \right|vB\)
- Hạt điện tích chuyển động theo quỹ đạo là đường tròn, lực từ đóng vai trò là lực hướng tâm.
Cách giải:
a) Áp dụng định lý biến thiên động năng: \(\frac{1}{2}m{v^2} = {\rm{eU}}\)
\( \Rightarrow {\rm{v}} = \sqrt {\frac{{2eU}}{m}} = \sqrt {\frac{{{{2.1,6.10}^{ - 19}}{{.2,7.10}^3}}}{{{{9,11.10}^{ - 31}}}}} \approx {3,08.10^7}\left( {{\rm{m/s}}} \right)\)
\( \to \) a đúng.
b) Electron lệch xuống dưới nên lực điện ngược hướng Oy mà \(\left\{ {\begin{array}{*{20}{l}}{\vec F = q\vec E}\\{q < 0}\end{array} \Rightarrow \vec E} \right.\) ngược hướng với \(\vec F \Rightarrow \vec E \uparrow \uparrow \overrightarrow {Oy} \)
\( \to \) b sai.
c) Từ hình a ta có:
\(y = \frac{1}{2}a{t^2} = \frac{1}{2}\frac{{qE}}{m}{\left( {\frac{x}{v}} \right)^2} \Rightarrow E = \frac{{2m{v^2}\left| y \right|}}{{\left| q \right|.{x^2}}}\) và quỹ đạo là một cung parabol.
Quỹ đạo của e được mô tả ở hình b là một cung tròn.
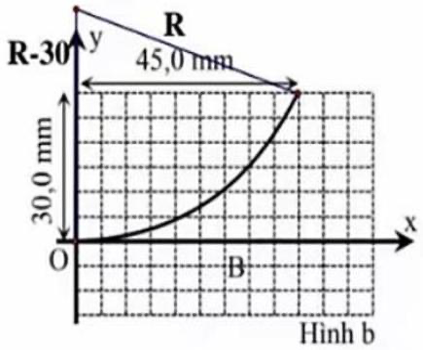
\( \to \) c sai.
d) Ta có: \(R - 30 = \sqrt {{R^2} - {{45}^2}} \Rightarrow R = 48,75\left( {{\rm{mm}}} \right)\)
Định luật II Newton: \(f = ma \Rightarrow \left| q \right|vB = \frac{{m{v^2}}}{R} \Rightarrow B = \frac{{mv}}{{\left| q \right|R}}\)
Để chùm e không bị lệch khỏi phương ban đầu thì lực điện phải cân bằng với lực từ:
\(\left| q \right|{v_d}B = \left| q \right|E \Rightarrow {v_d}\frac{{mv}}{R} = \frac{{2m{v^2}\left| y \right|}}{{{x^2}}} \Rightarrow \frac{{{v_d}}}{v} = \frac{{2R\left| y \right|}}{{{x^2}}}\)
Độ biến thiên động năng bằng công của lực điện: \(\left\{ {\begin{array}{*{20}{l}}{\frac{1}{2}mv_d^2 = e{U_d}}\\{\frac{1}{2}m{v^2} = eU}\end{array}} \right.\)
\( \Rightarrow \frac{{{U_d}}}{U} = {\left( {\frac{{{v_d}}}{v}} \right)^2} = {\left( {\frac{{2R\left| y \right|}}{{{x^2}}}} \right)^2}\)
\( \Rightarrow \frac{{{U_d}}}{{2,7}} = {\left( {\frac{{2.48,75.30}}{{{{81}^2}}}} \right)^2}\)
\( \Rightarrow {U_d} \approx 0,5366\left( {kV} \right) = 536,6\left( V \right)\)
\( \to \) d sai.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
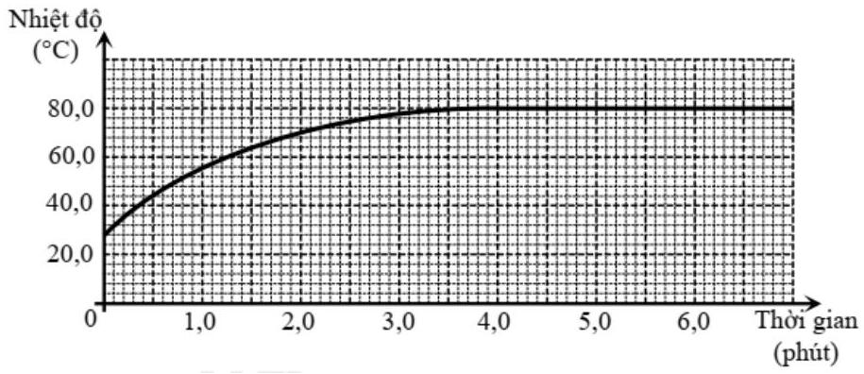
- Lý thuyết về thí nghiệm đo nhiệt dung riêng.
- Công thức tính giá trị trung bình và sai số của phép đo, cách ghi kết quả đo.
- Áp dụng phương trình cân bằng nhiệt.
Cách giải:
a) Trình tự thí nghiệm: Cân khối lượng của nước rồi cho vào nhiệt lượng kế; Đo nhiệt độ ban đầu của nước và bộ dụng cụ kèm theo; Cân khối lượng của khối nước đá rồi cho vào nhiệt lượng kế; Đo nhiệt độ ổn định của nước khi nước đá vừa tan hết.
\( \to \) a đúng.
b) Để giữ cho nhiệt độ nóng chảy của nước đá không thay đổi trong suốt quá trình thí nghiệm phải giữ áp suất tác dụng lên viên đá không đổi.
\( \to \) b đúng.
c) Khối lượng nước trung bình:
\({\overline m _n} = \frac{{{m_{n1}} + {m_{n2}} + {m_{n3}}}}{3}\)
\( \Rightarrow {\overline m _n} = \frac{{192,92 + 192,94 + 192,91}}{3}\)
\( \Rightarrow {\overline m _n} = \frac{{57877}}{{300}} \approx 192,92\left( {\rm{g}} \right)\)
Sai số tuyệt đối của phép đo:
\({\rm{\Delta }}{m_n} = \overline {{\rm{\Delta }}{m_n}} + {\rm{\Delta }}{m_{dc}} = \overline {{\rm{\Delta }}{m_n}} + 0,01{\rm{\;g}}\)
Kết quả phép đo khối lượng nước sử dụng trong thí nghiệm là \({m_n} = 192,92 \pm {\rm{\Delta }}{m_n}\)
\( \to \) c sai.
d) Ta có:
\(\overline {{m_d}} = \frac{{{m_{d1}} + {m_{d2}} + {m_{d3}}}}{3} = \frac{{36,71 + 36,74 + 36,75}}{3} = \frac{{551}}{{15}}\left( {\rm{g}} \right)\)
Phương trình cân bằng nhiệt:
\({m_d}\left( {\lambda + ct} \right) = \left( {{m_n}c + {C_0}} \right)\left( {t - {t_0}} \right)\)
\( \Rightarrow \frac{{551}}{{15}}{.10^{ - 3}}\left( {\lambda + 4180.15,5} \right) = \left( {\frac{{57877}}{{300}}{{.10}^{ - 3}}.4180 + 41,9} \right).\left( {32 - 15,5} \right)\)
\( \Rightarrow \lambda \approx {3,16.10^5}\left( {{\rm{J}}/{\rm{kg}}.{\rm{K}}} \right)\)
\( \to \) d đúng.
Lời giải
Phương pháp:
Tốc độ hóa hơi trung bình trong khoảng thời gian trên: \(\frac{{{\rm{\Delta }}m}}{{{\rm{\Delta }}t}}\).
Cách giải:
Tốc độ hóa hơi trung bình của khối nước thí nghiệm trong khoảng thời gian trên:
\(\frac{{{\rm{\Delta }}m}}{{{\rm{\Delta }}t}} = \frac{{1873 - 1773}}{{162,05}} \approx 0,62\left( {{\rm{g}}/{\rm{s}}} \right)\)
Đáp án: 0,62.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. có giá trị không đổi.
B. tăng dần theo thời gian.
C. giảm dần theo thời gian.
D. tăng sau đó giảm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. tối thiểu.
B. bằng không.
C. tối đa.
D. bằng hai lần giá trị tối thiểu
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. động năng của các phân tử tăng, thế năng không đổi.
B. động năng của các phân tử tăng, thế năng giảm.
C. động năng của các phân tử không đổi, thế năng tăng.
D. động năng và thế năng của các phân tử đều tăng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{{{V_0}}}{{{{1,1}^2}}}\).
B. \(\frac{{{V_0}}}{{1,1}}\).
C. \(1,1{V_0}\).
D. \({1,1^2}{V_0}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo