Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó t là thời gian tính bằng giây. Hỏi thời gian bằng bao nhiêu để số lượng vi khuẩn đạt cực đại.
Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con), trong đó t là thời gian tính bằng giây. Hỏi thời gian bằng bao nhiêu để số lượng vi khuẩn đạt cực đại.
Quảng cáo
Trả lời:
Có \(N'\left( t \right) = \frac{{100\left( {100 + {t^2}} \right) - 200{t^2}}}{{{{\left( {100 + {t^2}} \right)}^2}}}\)\( = \frac{{{{100}^2} - 100{t^2}}}{{{{\left( {100 + {t^2}} \right)}^2}}}\);
\(N'\left( t \right) = 0 \Leftrightarrow t = 10\) (vì t > 0).
Ta có bảng biến thiên
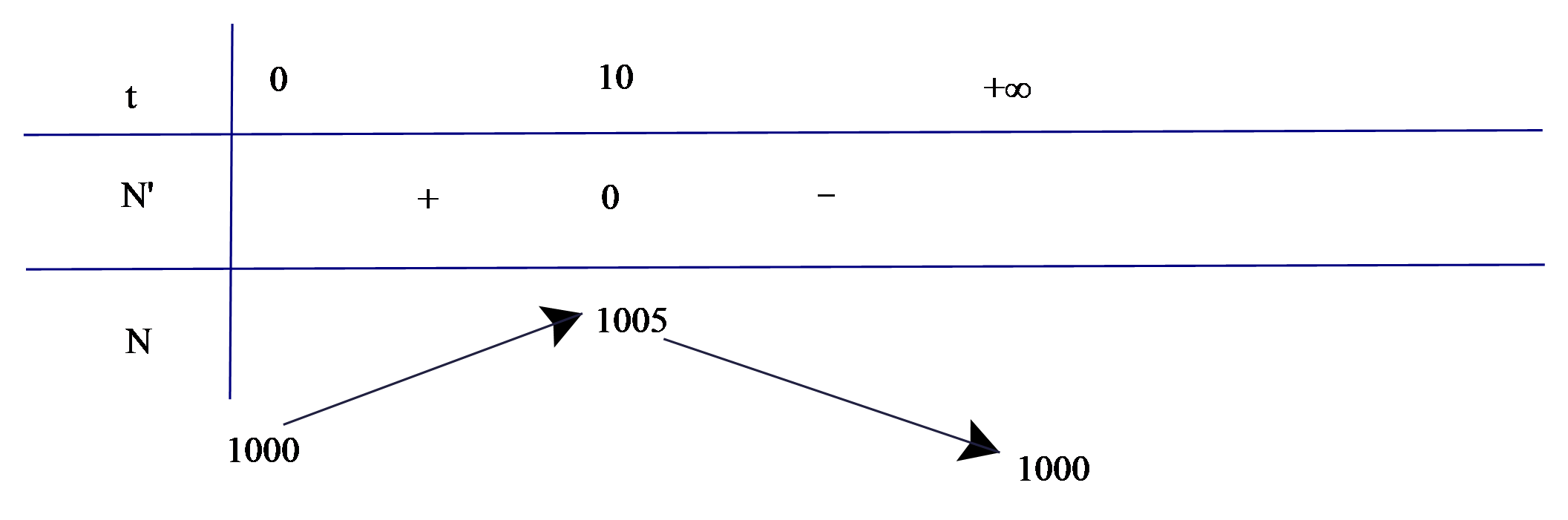
Dựa vào bảng biến thiên, ta có số lượng vi khuẩn đạt cực đại khi t = 10 giây.
Trả lời: 10.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
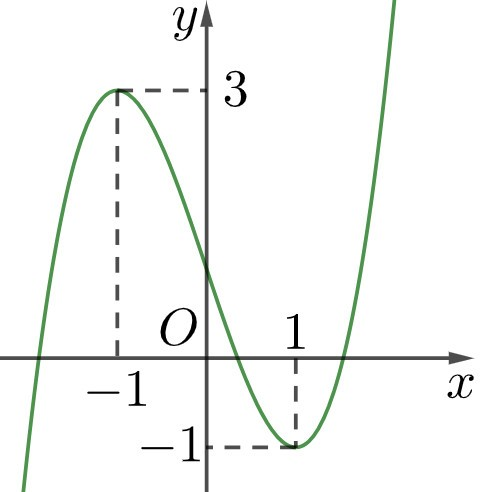
a) Hàm số \(y = f(x)\) đồng biến trên các khoảng \(( - \infty ; - 1)\) và \((1; + \infty ).\)
b) Giá trị cực đại là y = 3, giá trị cực tiểu là y = –1.
Do đó tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho là 3 – 1 = 2.
c) Hàm số \(y = f(x)\)có hai cực trị là \(x = \pm 1.\)
d) Gọi \[d:y = ax + b\] là đường thẳng qua hai điểm cực trị \[A( - 1;3),B(1; - 1).\]
\[A,B \in d \Rightarrow \left\{ \begin{array}{l} - a + b = 3\\a + b = - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 2\\b = 1\end{array} \right. \Rightarrow d:y = - 2x + 1\].
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.
Lời giải
Tập xác định \(\mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có \(y' = - \frac{1}{{{{\left( {x + 2} \right)}^2}}} < 0,\forall x \ne - 2\).
Do đó hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
Đáp án: a) Sai; b) Đúng; c) Sai; d) Đúng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.