Kết quả đo khối lượng của 30 củ khoai tây ở nông trường được biểu diễn ở biểu đồ dưới đây

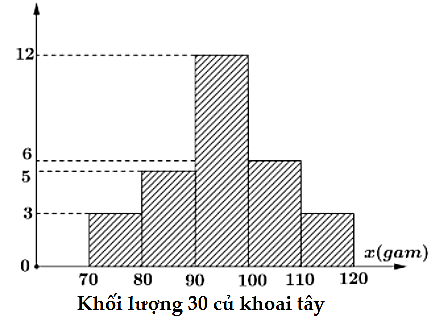
Tính gần đúng đến hàng phần chục mốt của mẫu số liệu trên.

Cho cấp số nhân \(\left( {{u_n}} \right)\) có các số hạng thỏa mãn: \(\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right.\)

a) Tìm số hạng đầu và công bội của cấp số nhân.

b) Hỏi tổng bao nhiêu số hạng đầu tiên bằng 3069?

c) Số 12288 là số hạng thứ mấy?

Tính tổng tất cả các số hạng của một cấp số nhân có số hạng đầu là \(\frac{1}{2}\), số hạng thứ tư là \(32\) và số hạng cuối là \(2048\)?

Tìm số hạng đầu tiên, công sai, số hạng thứ \(20\) và tổng của \(20\) số hạng đầu tiên của các cấp số cộng sau, biết rằng:

a) \(\left\{ \begin{array}{l}{u_5} = 19\\{u_9} = 35\end{array} \right.\);                                                                       

b) \(\left\{ \begin{array}{l}{u_3} + {u_5} = 14\\{s_{12}} = 129\end{array} \right.\).

Giải các phương trình sau

a) \(\tan \left( {2x - 1} \right) = \tan \left( { - x + \frac{\pi }{3}} \right)\);                                 b) \(\cot \left( {2x - \frac{\pi }{3}} \right) = 1\).

Tìm nghiệm lớn nhất của phương trình \(2\cos 2x - 1 = 0\) trong đoạn \(\left[ {0;\pi } \right]\).

B. TỰ LUẬN

b) Cho \(\sin \alpha = \frac{3}{5}\)và \({\rm{90}}^\circ < \alpha < 180^\circ \). Tính giá trị của biểu thức \(E = \frac{{\cot \alpha - 2\tan \alpha }}{{\tan \alpha + 3\cot \alpha }}\) .

Giải các phương trình sau

a) \(\sin \left( {3x - \frac{{3\pi }}{4}} \right) = \sin \left( {\frac{\pi }{6} - x} \right)\);                             b) \(\cos \left( {2x + 25^\circ } \right) = - \frac{{\sqrt 2 }}{2}\).