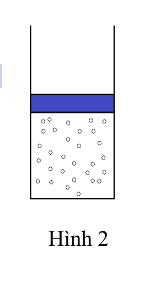
Trong môi trường không khí có nhiệt độ , áp suất 1 atm đặt thẳng đứng một bình hình trụ có bán kính đáy \(4,0\;{\rm{cm}}\), miệng bình phía trên để hở. Người ta đậy kín bình bằng một nắp khối lượng \(2,8\;{\rm{kg}}\) (Hình bên). Lấy \({\rm{g}} = 9,8\;{\rm{m}}/{{\rm{s}}^2}\). Cung cấp nhiệt để tăng nhiệt độ không khí trong bình, nhiệt độ nhỏ nhất của không khí trong bình để không khí có thể đẩy nắp bình lên và thoát ra ngoài gần nhất với giá trị nào sau đây?
Quảng cáo
Trả lời:
\(S = \pi {r^2} = \pi \cdot {0,04^2} = {1,6.10^{ - 3}}\pi \left( {{m^2}} \right)\)
|
\(p\) |
\(V\) |
\(T\) |
|
\({{\rm{p}}_0} = 101325\;{\rm{Pa}}\) |
|
\(27 + 273 = 300\;{\rm{K}}\) |
|
\({{\rm{p}}_0} + \frac{{{\rm{mg}}}}{{\rm{s}}} = 101325 + \frac{{2,8.9,8}}{{1,6 \cdot {{10}^{ - 3}}\pi }} \approx 106784\;{\rm{Pa}}\) |
|
\(\;{{\rm{T}}_2}\) |
\(\frac{p}{T} = \) const \( \Rightarrow \frac{{101325}}{{300}} = \frac{{106784}}{{{T_2}}} \Rightarrow {T_2} \approx 316\;{\rm{K}} \approx {43^^\circ }{\rm{C}}\). Chọn A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
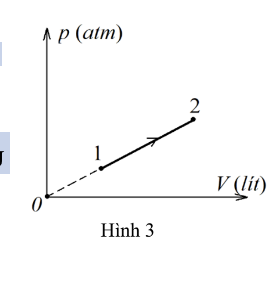
a) Đúng. Nhiệt độ tăng và áp suất không đổi
b) Sai. p giảm \( \Rightarrow {\rm{V}}\) tăng \( \Rightarrow \) dãn chứ không phải nén
c) Sai. Nhiệt độ không đổi nên nội năng không đổi
d) Đúng. Trạng thái 2 và 4 nằm trên đường đẳng tích
Lời giải
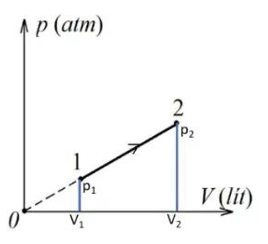
Diện tích hình thang bằng hiệu diện tích của 2 tam giác
\({A^\prime } = \frac{1}{2}{p_2}{V_2} - \frac{1}{2}{p_1}{V_1} = \frac{1}{2}nR\left( {{T_2} - {T_1}} \right)\)
\( = \frac{1}{2} \cdot 3,5 \cdot 8,31 \cdot 165 \approx 2,40 \cdot {10^3}\;{\rm{J}} = 2,40\;{\rm{kJ}}\)
Trả lời ngắn: 2,40
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.