Tính giá trị của biểu thức \(A = \cos \left( {\frac{\pi }{3} - x} \right)\cos \left( {\frac{\pi }{4} + x} \right) + \cos \left( {\frac{\pi }{6} + x} \right)\cos \left( {\frac{{3\pi }}{4} + x} \right)\) ta được \(A = \cos \frac{a}{b}\pi \) với \(\frac{a}{b}\) là phân số tối giản, \(a,b \in \mathbb{Z}\). Tính \(\frac{a}{b}\) (kết quả làm tròn đến hàng phần trăm).
Tính giá trị của biểu thức \(A = \cos \left( {\frac{\pi }{3} - x} \right)\cos \left( {\frac{\pi }{4} + x} \right) + \cos \left( {\frac{\pi }{6} + x} \right)\cos \left( {\frac{{3\pi }}{4} + x} \right)\) ta được \(A = \cos \frac{a}{b}\pi \) với \(\frac{a}{b}\) là phân số tối giản, \(a,b \in \mathbb{Z}\). Tính \(\frac{a}{b}\) (kết quả làm tròn đến hàng phần trăm).
Quảng cáo
Trả lời:
\(A = \cos \left( {\frac{\pi }{3} - x} \right)\cos \left( {\frac{\pi }{4} + x} \right) + \cos \left( {\frac{\pi }{6} + x} \right)\cos \left( {\frac{{3\pi }}{4} + x} \right)\)
\( = \frac{1}{2}\left[ {\cos \left( {\frac{\pi }{{12}} - 2x} \right) + \cos \frac{{7\pi }}{{12}}} \right] + \frac{1}{2}\left[ {\cos \left( { - \frac{{7\pi }}{{12}}} \right) + \cos \left( {\frac{{11\pi }}{{12}} + 2x} \right)} \right]\)
\( = \frac{1}{2}\left[ {\cos \left( {\frac{\pi }{{12}} - 2x} \right) + \cos \left( {\frac{{11\pi }}{{12}} + 2x} \right) + \cos \frac{{7\pi }}{{12}} + \cos \left( { - \frac{{7\pi }}{{12}}} \right)} \right]\)
\( = \frac{1}{2}\left( {0 + 2\cos \frac{{7\pi }}{{12}}} \right)\) (do \(\frac{{11\pi }}{{12}} + 2x + \frac{\pi }{{12}} - 2x = \pi \))
\( = \cos \frac{{7\pi }}{{12}}\).
Vậy \(\frac{a}{b} = \frac{7}{{12}} \approx 0,58\).
Trả lời: 0,58.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Biên độ của dao động thứ nhất bằng 3 cm.
b) Pha ban đầu của dao động thứ hai bằng \(\frac{\pi }{3}\).
c) \(\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\).
d) \(x\left( t \right) = {x_1}\left( t \right) + {x_2}\left( t \right)\)\( = 3\cos \left( {\frac{\pi }{4}t + \frac{{5\pi }}{6}} \right) + 3\cos \left( {\frac{\pi }{4}t + \frac{\pi }{3}} \right)\)
\( = 3.2\cos \left( {\frac{{\frac{\pi }{4}t + \frac{{5\pi }}{6} + \frac{\pi }{4}t + \frac{\pi }{3}}}{2}} \right)\cos \left( {\frac{{\frac{\pi }{4}t + \frac{{5\pi }}{6} - \frac{\pi }{4}t - \frac{\pi }{3}}}{2}} \right)\)
\( = 3.2.\frac{{\sqrt 2 }}{2}\cos \left( {\frac{\pi }{4}t + \frac{{7\pi }}{{12}}} \right)\)\( = 3\sqrt 2 \cos \left( {\frac{\pi }{4}t + \frac{{7\pi }}{{12}}} \right)\).
Suy ra biên độ và pha ban đầu của dao động tổng hợp lần lượt là \(3\sqrt 2 \) và \(\frac{{7\pi }}{{12}}\).
Đáp án: a) Đúng; b) Sai; c) Đúng; d) Đúng.
Lời giải
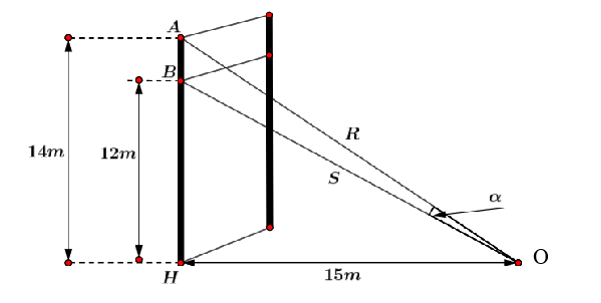
Ta có \(\alpha = \widehat {AOH} - \widehat {BOH}\).
Trong tam giác vuông \(AOH\) ta có \(\tan \widehat {AOH} = \frac{{AH}}{{OH}} = \frac{{14}}{{15}}\).
Trong tam giác vuông \(BOH\) ta có \(\tan \widehat {BOH} = \frac{{BH}}{{OH}} = \frac{{12}}{{15}} = \frac{4}{5}\).
Vậy \(\tan \alpha = \tan \left( {\widehat {AOH} - \widehat {BOH}} \right)\) \( = \frac{{\tan \widehat {AOH} - \tan \widehat {BOH}}}{{1 + \tan \widehat {AOH}.\tan \widehat {BOH}}} = \frac{{\frac{{14}}{{15}} - \frac{4}{5}}}{{1 + \frac{{14}}{{15}}.\frac{4}{5}}} = \frac{{10}}{{131}}\).
Suy ra a = 10; b = 131. Do đó \(a + b = 141\).
Trả lời: 141.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.