Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.
a) \(f\left( x \right) = \frac{{2x + 3}}{{x + 1}}\) trên đoạn \(\left[ {0;4} \right]\);
b) \(f\left( x \right) = \frac{{2{x^2} + 4x + 5}}{{{x^2} + 1}}\) trên \(\mathbb{R}\).
Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.
a) \(f\left( x \right) = \frac{{2x + 3}}{{x + 1}}\) trên đoạn \(\left[ {0;4} \right]\);
b) \(f\left( x \right) = \frac{{2{x^2} + 4x + 5}}{{{x^2} + 1}}\) trên \(\mathbb{R}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Có \(f'\left( x \right) = - \frac{1}{{{{\left( {x + 1} \right)}^2}}} < 0,\forall x \in \left[ {0;4} \right]\). Suy ra hàm số đã cho nghịch biến trên đoạn \([0;4]\).
Vậy \(\mathop {\max }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( 0 \right) = 3;\mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( 4 \right) = \frac{{11}}{5}\).
b) Có \(f'\left( x \right) = \frac{{ - 4{x^2} - 6x + 4}}{{{{\left( {{x^2} + 1} \right)}^2}}}\); \(f'\left( x \right) = 0 \Leftrightarrow - 4{x^2} - 6x + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = \frac{1}{2}\end{array} \right.\).
Bảng biến thiên
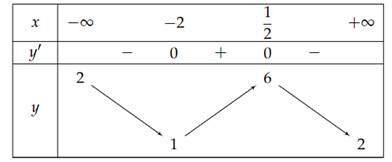
Dựa vào bảng biến thiên, ta có: \(\mathop {\min }\limits_\mathbb{R} f\left( x \right) = f\left( { - 2} \right) = 1;\mathop {\max }\limits_\mathbb{R} f\left( x \right) = f\left( {\frac{1}{2}} \right) = 6\).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {CB} \) là hai vectơ ngược hướng nên góc giữa chúng bằng 180°.
b) Hai vectơ \(\overrightarrow {BD} \) và \(\overrightarrow {BO} \) là hai vectơ cùng hướng nên góc giữa chúng là \(0^\circ \).
c) Ta có \(\left( {\overrightarrow {BA} ,\overrightarrow {CS} } \right) = \left( {\overrightarrow {CD} ,\overrightarrow {CS} } \right) = \widehat {SCD}\).
Áp dụng định lí côsin cho tam giác SCD có:
\(\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2SC.CD}} = \frac{{{{\left( {2a} \right)}^2} + {a^2} - {{\left( {2a} \right)}^2}}}{{2.2a.a}} = \frac{1}{4}\).
d) Ta có \(\overrightarrow {AO} .\overrightarrow {SD} = - \overrightarrow {OA} .\left( {\overrightarrow {OD} - \overrightarrow {OS} } \right) = - \overrightarrow {OA} .\overrightarrow {OD} + \overrightarrow {OA} .\overrightarrow {OS} = 0\) nên góc giữa hai vectơ \(\overrightarrow {AO} \) và \(\overrightarrow {SD} \) bằng 90°.
Đáp án: a) Sai; b) Sai; c) Đúng; d) Sai.
Câu 2
A. \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\].
B. \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\].
C. \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {DC} + \overrightarrow {AD} + \overrightarrow {BD} } \right)\].
D. \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {CD} } \right)\].
Lời giải
Ta có: \(\overrightarrow {IJ} \, = \,\,\overrightarrow {IA} + \,\overrightarrow {AJ} \)\( = \, - \frac{1}{2}\overrightarrow {AB} \, + \frac{1}{2}\left( {\overrightarrow {AC} \, + \,\overrightarrow {AD} } \right)\) \( = \,\frac{1}{2}\left( {\overrightarrow {BC} + \,\overrightarrow {AD} } \right)\)
\( = \,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BD} + \overrightarrow {CD} + \overrightarrow {DC} + \overrightarrow {BC} } \right)\) \( = \,\frac{1}{2}\left( {\overrightarrow {DC} + \overrightarrow {BD} + \overrightarrow {AD} } \right)\).
Vậy đẳng thức sai là \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {CD} } \right)\]. Chọn D.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\overrightarrow {BC} - \overrightarrow {{B_1}{C_1}} = \overrightarrow {{B_1}{A_1}} - \overrightarrow {BA} \).
B. \(\overrightarrow {AD} + \overrightarrow {{D_1}{C_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow {DC} \).
C. \(\overrightarrow {BC} + \overrightarrow {BA} + \overrightarrow {B{B_1}} = \overrightarrow {B{D_1}} \).
D. \(\overrightarrow {BA} + \overrightarrow {D{D_1}} + \overrightarrow {B{D_1}} = \overrightarrow {BC} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo