Cho \(\sin \alpha = \frac{1}{3}\) với \(90^\circ < \alpha < 180^\circ \).
a) Giá trị \(\sin \alpha .\cos \alpha < 0\).
b) \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}\).
c) \(\tan \alpha = \frac{{\sqrt 2 }}{4}\).
d) \(\frac{{6\sin \alpha + 3\sqrt 2 \cos \alpha }}{{2\sqrt 2 \tan \alpha + \sqrt 2 \cot \alpha }} = \frac{2}{5}\).
Cho \(\sin \alpha = \frac{1}{3}\) với \(90^\circ < \alpha < 180^\circ \).
a) Giá trị \(\sin \alpha .\cos \alpha < 0\).
b) \(\cos \alpha = - \frac{{2\sqrt 2 }}{3}\).
c) \(\tan \alpha = \frac{{\sqrt 2 }}{4}\).
d) \(\frac{{6\sin \alpha + 3\sqrt 2 \cos \alpha }}{{2\sqrt 2 \tan \alpha + \sqrt 2 \cot \alpha }} = \frac{2}{5}\).
Quảng cáo
Trả lời:
a) Vì \(90^\circ < \alpha < 180^\circ \) nên \(\cos \alpha < 0\). Suy ra \(\sin \alpha .\cos \alpha < 0\).
b) Có \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{1}{3}} \right)^2} = \frac{8}{9}\) \( \Rightarrow \cos \alpha = - \frac{{2\sqrt 2 }}{3}\) vì \(\cos \alpha < 0\).
c) Ta có \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{1}{3}:\frac{{ - 2\sqrt 2 }}{3} = - \frac{{\sqrt 2 }}{4}\).
d) \(\frac{{6\sin \alpha + 3\sqrt 2 \cos \alpha }}{{2\sqrt 2 \tan \alpha + \sqrt 2 \cot \alpha }} = \frac{{6\sin \alpha + 3\sqrt 2 \cos \alpha }}{{2\sqrt 2 \tan \alpha + \frac{{\sqrt 2 }}{{\tan \alpha }}}}\)\( = \frac{{6.\frac{1}{3} + 3\sqrt 2 .\frac{{ - 2\sqrt 2 }}{3}}}{{2\sqrt 2 .\frac{{ - \sqrt 2 }}{4} - \frac{{\sqrt 2 }}{{\frac{{\sqrt 2 }}{4}}}}}\)\( = \frac{2}{5}\).
Đáp án: a) Đúng; b) Đúng; c) Sai; d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số xe lớn và số xe nhỏ mà chủ trang trại cần thuê lần lượt là \(x;y\left( {x,y \in \mathbb{N}} \right)\).
Theo đề ta có hệ bất phương trình \(\left\{ \begin{array}{l}15x + 12y \ge 120\\5x + 2y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array} \right.\)
Miền nghiệm của hệ bất phương trình là miền trong của ngũ giác ABCDE (kể cả bờ) với \(A\left( {2;10} \right),B\left( {9;10} \right),C\left( {9;0} \right),D\left( {8;0} \right),E\left( {4;5} \right)\).
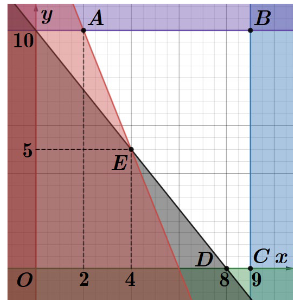
Theo đề bài ta có biểu thức biểu thị số tiền thuê xe là \(F = 500x + 350y\)(nghìn đồng).
Với A(2; 10) thì F = 4500;
Với B(9; 10) thì F = 8000;
Với C(9; 0) thì F = 4500;
Với D(8; 0) thì F = 4000;
Với E(4; 5) thì F = 3750.
Vậy số tiền thuê thấp nhất để chở 120 con bò sữa và 30 tấn thức ăn cho bò là 3750000 đồng khi thuê 4 xe lớn và 5 xe nhỏ.
Trả lời: 3750.
Câu 2
A. \(\left\{ \begin{array}{l}x + y - 1 \ge 0\\2x - y + 4 \le 0\end{array} \right.\).
Lời giải
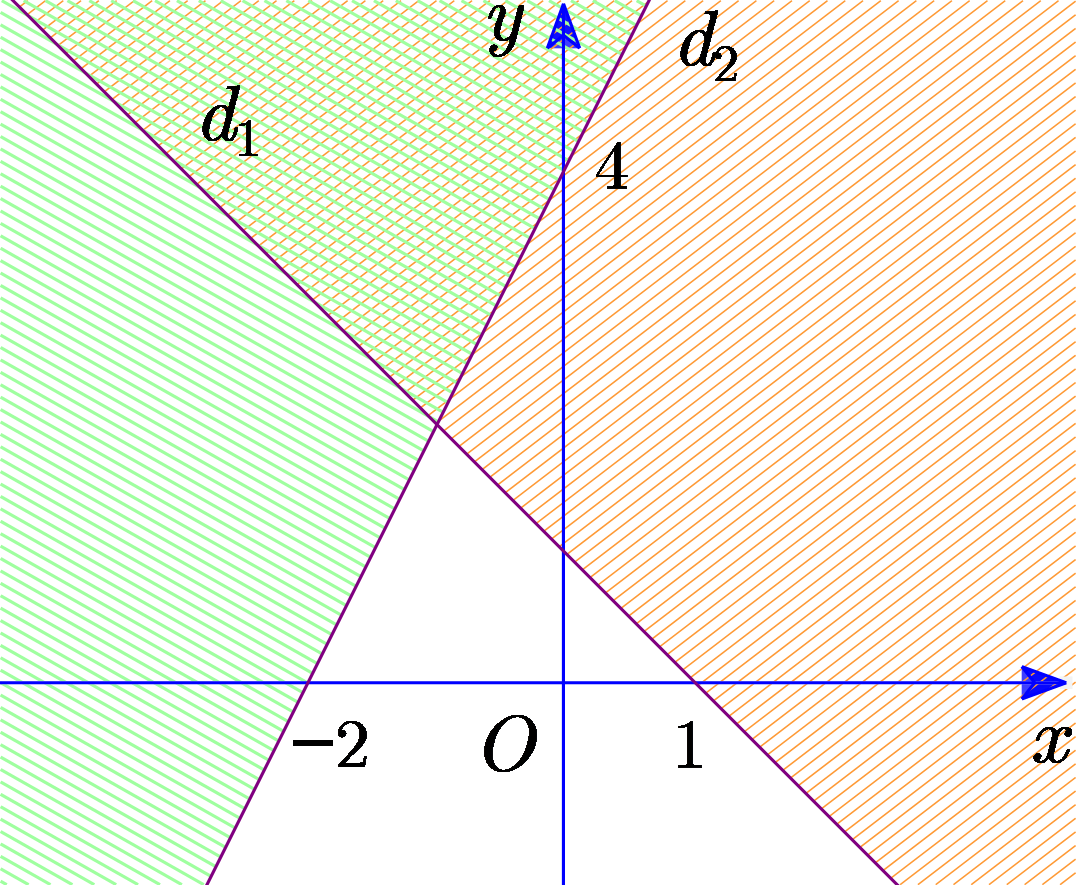
Đường thẳng d1 đi qua điểm (1; 0) và (0; 1) có phương trình là \(x + y - 1 = 0\).
Vì O(0; 0) không thuộc d1 thuộc vào miền nghiệm nên thay (0; 0) vào d1 ta có \( - 1 < 0\).
Suy ra \(x + y - 1 \le 0\).
Đường thẳng d2 đi qua điểm (−2; 0) và (0; 4) có phương trình \(2x - y + 4 = 0\).
Vì O(0; 0) không thuộc d2 thuộc miền nghiệm nên thay (0; 0) vào d2 ta có 4 > 0.
Suy ra \(2x - y + 4 \ge 0\).
Vậy miền không bị gạch chéo là miền nghiệm của bất phương trình \(\left\{ \begin{array}{l}x + y - 1 \le 0\\2x - y + 4 \ge 0\end{array} \right.\). Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
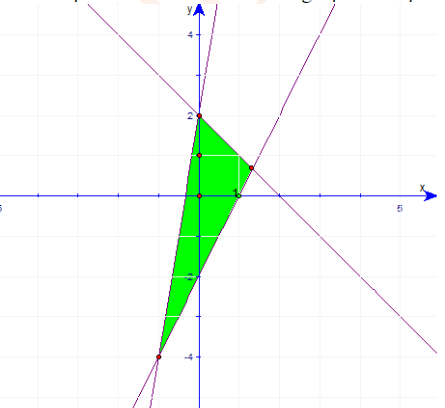
A. \(\left\{ \begin{array}{l}2x - y - 2 < 0\\x + y < 2\\6x - y + 2 > 0\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.