Cho tam giác nhọn \[ABC\] có \[AB < BC.\] Từ trung điểm \(M\) của cạnh \(AB\) kẻ đường thẳng song song với \(BC\) cắt cạnh \(AC\) tại \(N.\) Trên cạnh \(BC\) lấy điểm \(D\) sao cho \(BD = MN.\) Kẻ đường cao \[AH\left( {H \in BC} \right)\] của tam giác \[ABC\].

a) Tứ giác \(BMND\)là hình bình hành.                  

b) Tam giác \(AMH\) cân tại \(A\).

c) \(\widehat {AMN} = \frac{2}{3}\widehat {HMN}.\)    

d) Tứ giác \(DHMN\) là hình thang cân.

Hướng dẫn giải

Đáp số: 60.

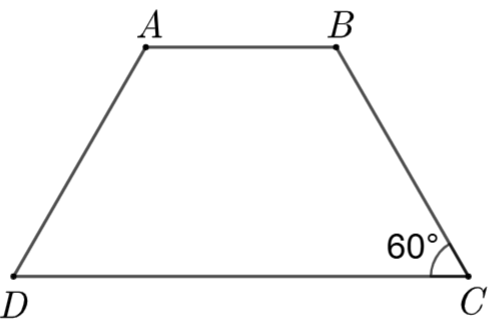
Vì \[ABCD\] là hình thang cân \(\left( {AB\,{\rm{//}}\,CD} \right)\) nên \(\widehat A = \widehat B\); \(\widehat C = \widehat D.\)

Hình thang \(ABCD\) có \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \) hay \[2\widehat A + 2\widehat C = 360^\circ \] nên \[\widehat A + \widehat C = 180^\circ .\]

Suy ra \[\widehat A = 180^\circ - \widehat C = 180^\circ - 60^\circ = 120^\circ .\]

Do đó \(\widehat A - \widehat C = 120^\circ - 60^\circ = 60^\circ .\)

Hướng dẫn giải

Đáp án:     a) Sai.        b) Đúng.    c) Đúng.     d) Sai.

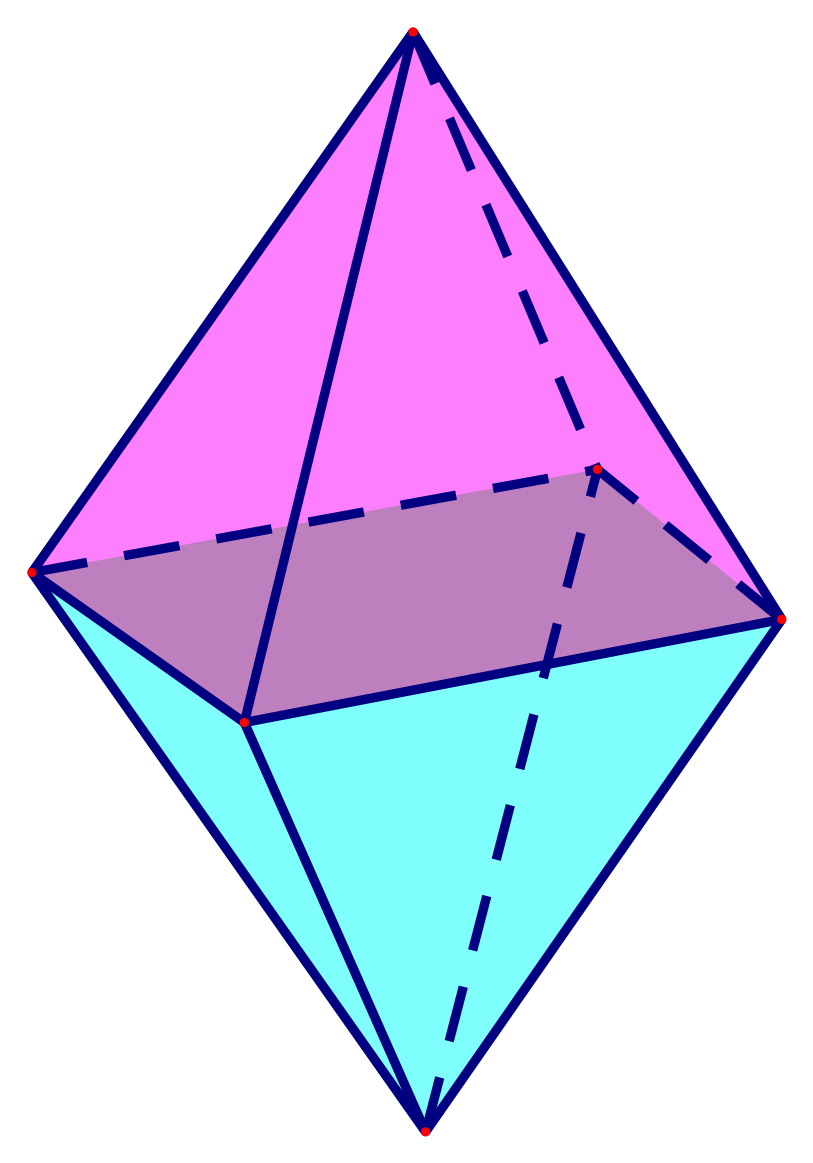
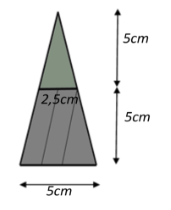
⦁ a) Công thức tính thể tích hình chóp tứ giác đều: \(V = \frac{1}{3} \cdot S \cdot h.\)

Trong đó \(V\) là thể tích, \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều). Do đó ý a) sai.

⦁ Chiều cao của mỗi hình chóp tứ giác đều là: \[30:2 = 15{\rm{ (cm)}}.\]Do đó ý b) đúng.

⦁ Thể tích của lòng đèn quả trám là: \(V = 2 \cdot \left( {\frac{1}{3} \cdot 20 \cdot 20 \cdot 15} \right) = 4\,\,000\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\). Do đó ý c) đúng.

⦁ Bạn Như muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị số mét thanh tre là:

\[50 \cdot \,\left( {20 \cdot 4 + 32 \cdot 8} \right) = 16\,\,800 (cm) = 168\,\,(m)\].

Vậy bạn Như muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị 168 mét thanh tre.

 Do đó ý d) sai.