Đề cương ôn tập cuối kì 1 Toán 8 Cánh diều cấu trúc mới (Đúng sai - Trả lời ngắn) có đáp án
25 người thi tuần này 4.6 789 lượt thi 20 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
Đáp án: a) Đúng. b) Đúng. c) Sai. d) Đúng.
⦁ Thể tích của bể bơi thứ nhất là: \(1,4 \cdot x \cdot y = 1,4xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\). Do đó ý a) đúng.
⦁ Diện tích đáy của bể bơi thứ nhất là: \(x \cdot y = xy{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Mà diện tích đáy của bê bơi thứ hai gấp 3 lần diện tích đáy của bể bơi thứ nhất.
Như vậy, diện tích đáy của bể bơi thứ hai là: \(3xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\). Do đó ý b) đúng.
⦁ Thể tích của bể bơi thứ hai là: \(1,6 \cdot 3xy = 4,8xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Vì \(4,8 < 5\) nên \(4,8xy < 5xy\).
Như vậy, thể tích của bể bơi thứ hai nhỏ hơn \(5xy{\rm{ }}\left( {{{\rm{m}}^3}} \right).\) Do đó ý c) sai.
⦁ Tổng thể tích hai bể bơi là: \(4,8xy + 1,4xy = 6,2xy{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
Thể tích nước cần bơm đầy hai bể bơi chính bằng tổng thể tích của của hai bể bơi và bằng \(6,2xy{\rm{ }}\left( {{{\rm{m}}^3}} \right).\) Do đó ý d) đúng.
Lời giải
Hướng dẫn giải
Đáp án: a) Sai. b) Sai. c) Đúng. d) Đúng.
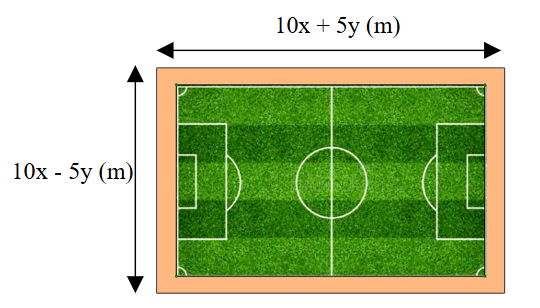
⦁ Vì mỗi cạnh chừa lại 3 m làm lối đi nên chiều dài của mặt sân trồng cỏ là:
\(10x + 5y - 2.3 = 10x + 5y - 6{\rm{ }}\left( {\rm{m}} \right).\)
Do đó ý a) sai.
⦁ Vì mỗi cạnh chừa lại 3 m làm lối đi nên chiều rộng của mặt sân trồng cỏ là:
\(10x - 5y - 2.3 = 10x - 5y - 6{\rm{ }}\left( {\rm{m}} \right).\)
Do đó ý b) sai.
⦁ Biểu thức biểu thị diện tích của mặt sân trồng cỏ là:
\(\left( {10x - 5y - 6} \right)\left( {10x + 5y - 6} \right) = 100{x^2} - 25{y^2} - 120x + 36{\rm{ }}\left( {{{\rm{m}}^2}} \right)\)
Do đó ý c) đúng.
⦁ Thay \(x = 9{\rm{ }}\left( {\rm{m}} \right),y = 3{\rm{ }}\left( {\rm{m}} \right)\) vào biểu thức biểu thị diện tích của mặt sân trồng cỏ, ta được:
\(S = {100.9^2} - {25.3^2} - 120.9 + 36 = 6{\rm{ }}831{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Do đó ý d) đúng.
Lời giải
Hướng dẫn giải
Đáp án: a) Đúng. b) Sai. c) Sai. d) Đúng.
⦁ Ta có \(A = 2xy\left( {x{y^2} - 3{x^2}y + 1} \right)\)
\( = 2{x^2}{y^3} - 6{x^3}{y^2} + 2xy\).
Đa thức \[A\] có bậc là 8. Do đó ý a) đúng.
⦁ Ta có \[B = \left( {12{x^4}{y^5} - 36{x^5}{y^4} + 6{x^3}{y^3}} \right):6{x^2}{y^2}\]
\[ = 12{x^4}{y^5}:\left( {6{x^2}{y^2}} \right) - 36{x^5}{y^4}:\left( {6{x^2}{y^2}} \right) + 6{x^3}{y^3}:\left( {6{x^2}{y^2}} \right)\]
\[ = 2{x^2}{y^3} - 6{x^3}{y^2} + xy\].
Khi đó, hệ số tự do của đa thức \(B\) là 0. Do đó ý b) sai.
⦁ Thay \[x = - 1\,;\,\,y = 1\] vào biểu thức \(B\), ta có:
\[B = 2 \cdot {\left( { - 1} \right)^2} \cdot {1^3} - 6 \cdot {\left( { - 1} \right)^3} \cdot {1^2} + \left( { - 1} \right) \cdot 1 = 2 + 6 - 1 = 7\].
Vậy với \[x = - 1\,;\,\,y = 1\] thì \(B = 7\). Do đó ý c) sai.
⦁ Ta có \(A = M + B\)
Suy ra \(M = A - B\)
\( = 2{x^2}{y^3} - 6{x^3}{y^2} + 2xy - \left( {2{x^2}{y^3} - 6{x^3}{y^2} + xy} \right)\)
\( = 2{x^2}{y^3} - 6{x^3}{y^2} + 2xy - 2{x^2}{y^3} + 6{x^3}{y^2} - xy\)
\( = \left( {2{x^2}{y^3} - 2{x^2}{y^3}} \right) + \left( { - 6{x^3}{y^2} + 6{x^3}{y^2}} \right) + \left( {2xy - xy} \right)\)\( = xy.\)
Như vậy, \(M\) là một đơn thức. Do đó ý d) đúng.
Lời giải
Hướng dẫn giải
Đáp án: a) Sai. b) Đúng. c) Sai. d) Sai.
⦁ Ta có \(A = \left( {{a^3} - {b^3}} \right) + \left( {5ab + 5{a^2} + 5{b^2}} \right)\)
\( = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) + 5\left( {{a^2} + ab + {b^2}} \right)\)
\( = \left( {{a^2} + ab + {b^2}} \right)\left( {a - b + 5} \right)\).
Do đó ý a) sai.
⦁ Với \(a - b = - 5\) ta có: \(A = \left( {{a^2} + ab + {b^2}} \right)\left( {5 - 5} \right) = 0.\) Do đó ý b) đúng.
⦁ Với \(a - b = 10\) ta có: \(A = \left( {{a^2} + ab + {b^2}} \right)\left( {10 - 5} \right) = 5\left( {{a^2} + ab + {b^2}} \right) \vdots 5.\) Do đó ý c) sai.
⦁ Vì \({a^2} + {b^2} = - ab\) nên \({a^2} + ab + {b^2} = 0.\)
Với \({a^2} + ab + {b^2} = 0\) ta có: \(A = 0\left( {a - b + 5} \right) = 0.\) Do đó ý d) sai.
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Sai. b) Sai. c) Đúng. d) Đúng.
⦁ Điều kiện để hàm số trên là hàm số bậc nhất là \(2 - m \ne 0\) suy ra \(m \ne 2\). Do đó ý a) sai.
⦁ Với \(m = - 1\), ta có: \(\left( d \right):y = 3x - 4\).
Thay \(x = 0,y = 4\) vào \(\left( d \right):y = 3x - 4\), ta được: \(3.0 - 4 = 4\) hay \( - 4 = 4\) (vô lí).
Như vậy, với \(m = - 1\) thì đồ thị hàm số \(\left( d \right)\) không đi qua điểm \(A\left( {0;4} \right).\) Do đó ý b) sai.
⦁ Để đường thẳng \(\left( d \right)\) song song với \(\left( {d'} \right):y = - x + m - 3\) thì \(\left\{ \begin{array}{l}2 - m = - 1\\3m - 1 \ne m - 3\end{array} \right.\) hay \(\left\{ \begin{array}{l}m = 3\\m \ne - 1\end{array} \right.\).
Như vậy, \(m = 3.\) Do đó ý c) đúng.
⦁ Nhận thấy đường thẳng \(\left( {d''} \right):y = - x + 2\) luôn cắt trục tung tại điểm có tung độ là \(2.\)
Đường thẳng \(\left( d \right)\) luôn cắt trục tung tại điểm có tung độ là \(3m - 1\).
Do đó, để \(\left( d \right)\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung thì \(2 = 3m - 1\).
Suy ra \(m = 1.\) Do đó ý d) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
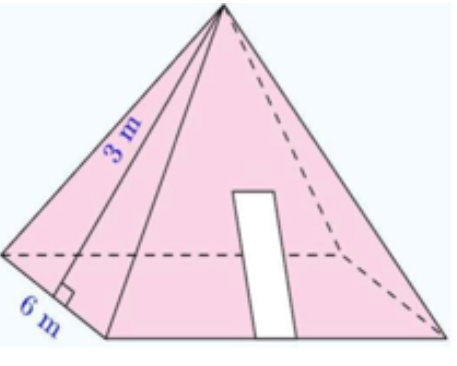
Hình vẽ dưới đây mô tả một khối bê tông mác 200 dùng trong việc xây cầu. Khối bê tông đó gồm hai phần: phần dưới có dạng hình lập phương với độ dài cạnh bằng \[1{\rm{ m}}\,;\] phần trên có dạng hình chóp tứ giác đều với chiều cao bằng \[0,6\,\,{\rm{m}}.\] Biết rằng \(1{\rm{ }}{{\rm{m}}^3}\) bê tông mác 200 cần khoảng \[350,55\,\,{\rm{kg}}\] xi măng và \[185\,\,l\] nước.
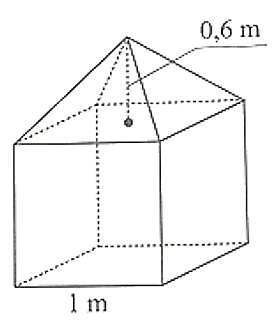
a) Thể tích phần trên (có dạng hình chóp tứ giác đều) của khối bê tông là \(0,2{\rm{ c}}{{\rm{m}}^3}.\)
b) Thể tích của khối bê tông là \(1,2{\rm{ c}}{{\rm{m}}^3}.\)
c) Khối lượng xi măng cần dùng để làm khối bê tông đó là \[0,5\] tấn.
d) Lượng nước cần dùng để làm khối bê tông đó là \(0,185{\rm{ }}{{\rm{m}}^3}.\)
Hình vẽ dưới đây mô tả một khối bê tông mác 200 dùng trong việc xây cầu. Khối bê tông đó gồm hai phần: phần dưới có dạng hình lập phương với độ dài cạnh bằng \[1{\rm{ m}}\,;\] phần trên có dạng hình chóp tứ giác đều với chiều cao bằng \[0,6\,\,{\rm{m}}.\] Biết rằng \(1{\rm{ }}{{\rm{m}}^3}\) bê tông mác 200 cần khoảng \[350,55\,\,{\rm{kg}}\] xi măng và \[185\,\,l\] nước.

b) Thể tích của khối bê tông là \(1,2{\rm{ c}}{{\rm{m}}^3}.\)
c) Khối lượng xi măng cần dùng để làm khối bê tông đó là \[0,5\] tấn.
d) Lượng nước cần dùng để làm khối bê tông đó là \(0,185{\rm{ }}{{\rm{m}}^3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
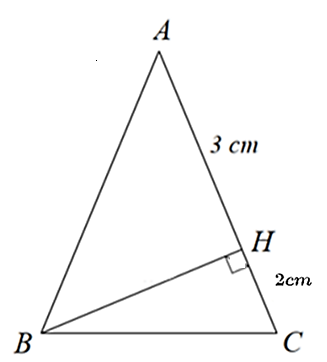
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\,,\) đường cao \(AH\,.\) Từ \(H\) kẻ \(HM \bot AB\,\,\left( {M \in AB} \right)\,.\) Kẻ \(HN \bot AC\,\,\left( {N \in AC} \right)\,.\) Trên tia đối của tia \[MH\] lấy điểm \[P\] sao cho \[M\] là trung điểm của \[PH.\] Gọi \(I\) là trung điểm của \(HC\,,\) lấy \(K\) trên tia \(AI\) sao cho \(I\) là trung điểm của \(AK;\,\,MN\) cắt \(AH\) tại \(O,\) \(CO\) cắt \(AK\) tại \(D.\)
a) \(\widehat {HKC} = \frac{1}{2}\widehat {HAC}\).
b) Tứ giác \[AMHN\] là hình chữ nhật.
c) Tứ giác \(MNCK\) là hình thang vuông.
d) \(AK = 2AD\).
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\,,\) đường cao \(AH\,.\) Từ \(H\) kẻ \(HM \bot AB\,\,\left( {M \in AB} \right)\,.\) Kẻ \(HN \bot AC\,\,\left( {N \in AC} \right)\,.\) Trên tia đối của tia \[MH\] lấy điểm \[P\] sao cho \[M\] là trung điểm của \[PH.\] Gọi \(I\) là trung điểm của \(HC\,,\) lấy \(K\) trên tia \(AI\) sao cho \(I\) là trung điểm của \(AK;\,\,MN\) cắt \(AH\) tại \(O,\) \(CO\) cắt \(AK\) tại \(D.\)
a) \(\widehat {HKC} = \frac{1}{2}\widehat {HAC}\).
b) Tứ giác \[AMHN\] là hình chữ nhật.
c) Tứ giác \(MNCK\) là hình thang vuông.
d) \(AK = 2AD\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.