Cho \(\Delta ABC\) cân tại \(A\) như hình vẽ dưới đây. Hỏi tỉ số \(\frac{{{S_{ABH}}}}{{{S_{BHC}}}}\) bằng bao nhiêu? (Kết quả ghi dưới dạng số thập phân)
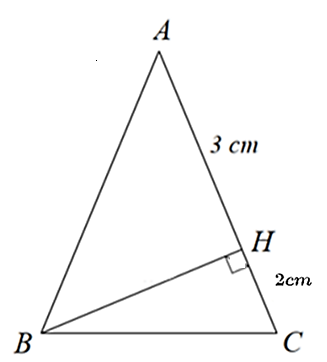
Cho \(\Delta ABC\) cân tại \(A\) như hình vẽ dưới đây. Hỏi tỉ số \(\frac{{{S_{ABH}}}}{{{S_{BHC}}}}\) bằng bao nhiêu? (Kết quả ghi dưới dạng số thập phân)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: \(1,5\).
Ta có: \(AC = AH + HC = 3 + 2 = 5{\rm{ }}\left( {{\rm{cm}}} \right)\).
Vì tam giác \(ABC\) cân tại \(A\) nên ta có \(AB = AC = 5{\rm{ cm}}\).• Áp dụng định lí Pythagore vào tam giác \(BHA\), ta có: \(B{H^2} + H{A^2} = A{B^2}\).
Suy ra \(B{H^2} = A{B^2} - H{A^2}\)\( = {5^2} - {3^2} = 16\) nên \(BH = 4\) cm.
• Diện tích tam giác \(ABH\) là: \(\frac{1}{2} \cdot 4 \cdot 3 = 6{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Diện tích tam giác \(BHC\) là: \(\frac{1}{2} \cdot 4 \cdot 2 = 4{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Do đó, ta có: \(\frac{{{S_{ABH}}}}{{{S_{BHC}}}} = \frac{6}{4} = \frac{3}{2} = 1,5\).
Vậy \(\frac{{{S_{ABH}}}}{{{S_{BHC}}}} = 1,5\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp số: 60.
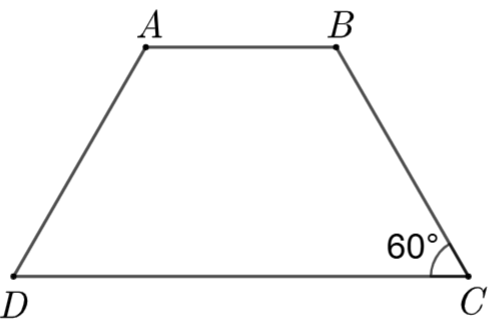
Vì \[ABCD\] là hình thang cân \(\left( {AB\,{\rm{//}}\,CD} \right)\) nên \(\widehat A = \widehat B\); \(\widehat C = \widehat D.\)
Hình thang \(ABCD\) có \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \) hay \[2\widehat A + 2\widehat C = 360^\circ \] nên \[\widehat A + \widehat C = 180^\circ .\]
Suy ra \[\widehat A = 180^\circ - \widehat C = 180^\circ - 60^\circ = 120^\circ .\]
Do đó \(\widehat A - \widehat C = 120^\circ - 60^\circ = 60^\circ .\)
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Sai. b) Sai. c) Đúng. d) Đúng.
⦁ Điều kiện để hàm số trên là hàm số bậc nhất là \(2 - m \ne 0\) suy ra \(m \ne 2\). Do đó ý a) sai.
⦁ Với \(m = - 1\), ta có: \(\left( d \right):y = 3x - 4\).
Thay \(x = 0,y = 4\) vào \(\left( d \right):y = 3x - 4\), ta được: \(3.0 - 4 = 4\) hay \( - 4 = 4\) (vô lí).
Như vậy, với \(m = - 1\) thì đồ thị hàm số \(\left( d \right)\) không đi qua điểm \(A\left( {0;4} \right).\) Do đó ý b) sai.
⦁ Để đường thẳng \(\left( d \right)\) song song với \(\left( {d'} \right):y = - x + m - 3\) thì \(\left\{ \begin{array}{l}2 - m = - 1\\3m - 1 \ne m - 3\end{array} \right.\) hay \(\left\{ \begin{array}{l}m = 3\\m \ne - 1\end{array} \right.\).
Như vậy, \(m = 3.\) Do đó ý c) đúng.
⦁ Nhận thấy đường thẳng \(\left( {d''} \right):y = - x + 2\) luôn cắt trục tung tại điểm có tung độ là \(2.\)
Đường thẳng \(\left( d \right)\) luôn cắt trục tung tại điểm có tung độ là \(3m - 1\).
Do đó, để \(\left( d \right)\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung thì \(2 = 3m - 1\).
Suy ra \(m = 1.\) Do đó ý d) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập