Câu hỏi:

19/09/2025 2

Cho hình chữ nhật $ABCD$, kẻ $AH,CK$ vuông góc với $BD$ $\left( {H,\,\,K \in BD} \right)$.

     a) Chứng minh $DH = BK$.

     b) Chứng minh tứ giác $AHCK$ là hình bình hành.

     c) Gọi $E$ là điểm đối xứng với $A$ qua $H$. Chứng minh $DECB$ là hình thang cân.

Xem lời giải

Câu hỏi trong đề: Đề cương ôn tập cuối kì 1 Toán 8 Cánh diều cấu trúc mới có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

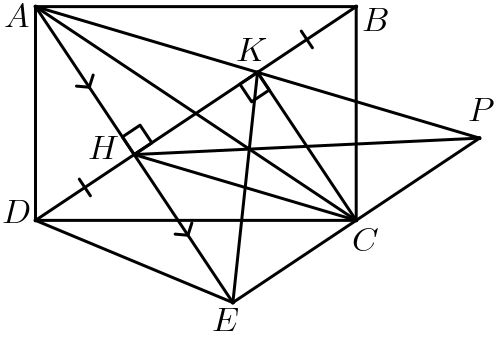
$Cho hình chữ nhật $ABCD$, kẻ $AH,CK$ vuông góc với $BD$ $\left( {H,\,\,K \in BD} \right)$. a) Chứng minh $DH = BK$. (ảnh 1)$

a) Do $ABCD$ là hình chữ nhật nên $AD = BC$ và $AD\,{\rm{//}}\,BC.$

Xét $\Delta AHD$ vuông tại $H$ và $\Delta CKB$ vuông tại $K$ có:

$AD = BC$ và $\widehat {ADH} = \widehat {CBK}$ (so le trong của $AD\,{\rm{//}}\,BC).$

Do đó $\Delta AHD = \Delta CKB$ (cạnh huyền – góc nhọn).

Suy ra $DH = BK$ (hai cạnh tương ứng).

b) Ta có $\Delta AHD = \Delta CKB$ (câu a) nên $AH = CK$.

Mặt khác: $AH \bot BD,\,\,CK \bot BD$ nên $AH\,{\rm{//}}\,CK$

Do đó tứ giác $AHCK$ là hình bình hành (dấu hiệu nhận biết).

c) Ta có: $AH = HE$ và $AH = CK$ nên $HE = CK$

Mà $HE\,{\rm{//}}\,CK$ ($AH\,{\rm{//}}\,CK$ và $E$ là điểm đối xứng với $A$ qua $H$)

Do đó tứ giác $CKHE$ là hình bình hành. Suy ra $HK\,{\rm{//}}\,CE$ hay $BD\,{\rm{//}}\,CE$ (1)

Xét $\Delta ADE$ có $DH$ là đường cao, vừa là trung tuyến nên $\Delta ADE$ cân tại $D$

Do đó $DH$ là đường phân giác của $\Delta ADE$, nên $\widehat {ADB} = \widehat {EDB}$

Mà $\widehat {ADB} = \widehat {CBD}$ nên $\widehat {EDB} = \widehat {CBD}$ (2)

Từ (1) và (2), suy ra tứ giác $CEDB$ là hình thang cân (dấu hiệu nhận biết hình thang cân).

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

(1,5 điểm) Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như hình bên.\

a) Tính thể tích không khí bên trong chiếc lều.
b) Tính số tiền mua vải phủ bốn phía và trải nền đất cho chiếc lều (coi các mép nối không đáng kể). Biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là $3,18\;\;{\rm{m}}$ và giá vải là $15\,\,000$ đồng/m². Ngoài ra, nếu mua vải với hóa đơn trên $20$ m² thì được giảm giá $5\% $ trên tổng hóa đơn.

Xem đáp án

Lời giải

Hướng dẫn giải

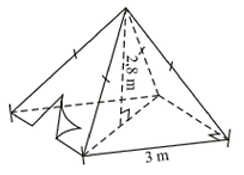
a) Diện tích đáy hình vuông của chiếc lều là:

Thể tích không khí bên trong chiếc lều là:

b) Diện tích xung quanh của chiếc lều là:

${S_{xq}} = \frac{1}{2} \cdot C \cdot d = \frac{1}{2} \cdot \left( {4 \cdot 3} \right) \cdot 3,18 = 19,08{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}$

Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:

$S = 9 + 19,08 = 28,08$ (m²).

Do $28,08 > 20$ nên số tiền mua vải được giảm giá $5\% $ trên tổng hóa đơn.

Vậy số tiền mua vải là: $28,08 \cdot 15\,\,000 \cdot \left( {100\% - 5\% } \right) = 400\,\,140$ (đồng).

Câu 2

Cho x và y thoả mãn: ${x^2} + 5{y^2} - 3xy - 3x - y + 5 = 0$. Tính giá trị của biểu thức:

$A = \frac{{{{\left( {x + y - 4} \right)}^{2222}} - {y^{2222}}}}{x}.$

Xem đáp án

Lời giải

Hướng dẫn giải

Ta có: ${x^2} + 5{y^2} - 3xy - 3x - y + 5 = 0$

Suy ra $2{x^2} + 10{y^2} - 6xy - 6x - 2y + 10 = 0$

${x^2} - 6xy + 9{y^2} + {x^2} - 6x + 9 + {y^2} - 2y + 1 = 0$

$\left( {{x^2} - 6xy + 9{y^2}} \right) + \left( {{x^2} - 6x + 9} \right) + \left( {{y^2} - 2y + 1} \right) = 0$

${\left( {x - 3y} \right)^2} + {\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 0$

Với mọi $x,\,\,y$ ta có: ${\left( {x - 3y} \right)^2} \ge 0,\,\,{\left( {x - 3} \right)^2} \ge 0,\,\,{\left( {y - 1} \right)^2} \ge 0$

Suy ra ${\left( {x - 3y} \right)^2} + {\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} \ge 0$

Do đó, để ${\left( {x - 3y} \right)^2} + {\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 0$ thì \[\left\{ {\begin{array}{*{20}{l}}{{{\left( {x - 3y} \right)}^2} = 0}\\{{{\left( {x - 3} \right)}^2} = 0}\\{{{\left( {y - 1} \right)}^2} = 0}\end{array}} \right.\] hay $\left\{ {\begin{array}{*{20}{l}}{x - 3y = 0}\\{x - 3 = 0}\\{y - 1 = 0}\end{array}} \right.$, tức là $\left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\end{array}} \right.$.

Thay $x = 3,\,\,y = 1$ vào biểu thức $A,$ ta được:

\[A = \frac{{{{\left( {3 + 1 - 4} \right)}^{2222}} - {1^{2222}}}}{3} = \frac{{ - 1}}{3}.\]

Câu 3