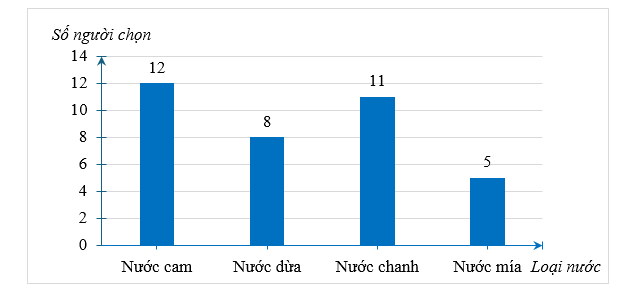
Biểu đồ dưới đây biểu diễn số lượng học sinh của một lớp chọn loại nước uống trong đợt liên hoan cuối năm. Biết mỗi học sinh chỉ chọn một loại nước uống và tất cả học sinh của lớp đều tham gia bình chọn.
Khẳng định nào sau đây là sai?
Biểu đồ dưới đây biểu diễn số lượng học sinh của một lớp chọn loại nước uống trong đợt liên hoan cuối năm. Biết mỗi học sinh chỉ chọn một loại nước uống và tất cả học sinh của lớp đều tham gia bình chọn.
Khẳng định nào sau đây là sai?
A. Lớp có 36 học sinh.
B. Loại nước được yêu thích nhất trong lớp là nước cam.
C. Số học sinh chọn nước dừa nhiều hơn số học sinh chọn nước mía.
D. Tổng số học sinh chọn nước dừa và nước mía ít hơn số học sinh chọn nước cam.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Số học sinh của lớp đó là: \(12 + 8 + 11 + 5 = 36\) (học sinh).
Loại nước được yêu thích nhất trong lớp là nước cam, với 12 học sinh lựa chọn.
Số học sinh chọn nước dừa nhiều hơn số học sinh chọn nước mía là \(8 - 5 = 3\) (học sinh).
Tổng số học sinh chọn nước dừa và nước mía là: \(8 + 5 = 13\) (học sinh), nhiều hơn số học sinh chọn nước cam. Do đó khẳng định D là sai.
Vậy ta chọn phương án D.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Biểu đồ tranh.
B. Biểu đồ cột.
C. Biểu đồ hình quạt tròn.
D. Biểu đồ đoạn thẳng.
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Khi muốn vẽ biểu đồ về tỉ lệ số học sinh của lớp 8A xếp loại học lực Tốt, Khá, Đạt, Chưa đạt ở cuối học kì I (biểu thị tỉ lệ phần trăm của từng loại số liệu so với tổng thể), ta sử dụng biểu đồ hình quạt tròn.
Câu 2
A. \(2,5{\rm{\;cm}}\).
B. \(5{\rm{\;cm}}\).
C. \(10{\rm{\;cm}}\).
D. \(15{\rm{\;cm}}\).
Lời giải
|
Hướng dẫn giải Đáp án đúng là: C Xét \(\Delta ABC\) vuông tại \(A,\) trung tuyến \(AM\) ứng với cạnh huyền \(BC\) nên \(AM = \frac{1}{2}BC\) hay \(BC = 2AM = 2 \cdot 5 = 10{\rm{\;(cm)}}{\rm{.}}\) |
|
Câu 3
A. \[1{\rm{ }}905,6\] tỉ đồng.
B. \[2{\rm{ }}113,3\] tỉ đồng.
C. \[563,8\] tỉ đồng.
D. \[635,71\] tỉ đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 4 cm.
B. \(\sqrt 6 \) cm.
C. 8 cm.
D. \(2\sqrt 2 \) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Biểu đồ tranh.
B. Biểu đồ cột.
C. Biểu đồ cột kép.
D. Biểu đồ đoạn thẳng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Số thành viên trong một gia đình.
B. Cân nặng (kg) của các học sinh lớp 8D.
C. Kết quả nhảy xa (mét) của 10 vận động viên.
D. Lượng mưa trung bình (mm) trong một tháng ở Thành phố Hồ Chí Minh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Từ nguồn có sẵn.
B. Quan sát.
C. Lập bảng hỏi.
D. Phỏng vấn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập